If the line drawn from (4,−1,2) meets a plane at right angles at the point (−10,5,4), find the equation of the plane.
To find the equation of the plane that is perpendicular to the line drawn from the point (4,−1,2) and meets the plane at the point (−10,5,4), we can follow these steps:
Step 1: Determine the Direction Ratios of the Line
The direction ratios of the line can be found using the two points: (4,−1,2) and (−10,5,4).
The direction ratios (or vector) from point (4,−1,2) to point (−10,5,4) can be calculated as follows:
Direction Ratios=(−10−4,5−(−1),4−2)=(−14,6,2)
Step 2: Use the Point-Normal Form of the Plane Equation
The equation of a plane can be expressed in the form:
a(x−x1)+b(y−y1)+c(z−z1)=0
where (x1,y1,z1) is a point on the plane and (a,b,c) are the direction ratios of the normal to the plane.
Here, we can take the point (−10,5,4) as (x1,y1,z1) and the direction ratios (−14,6,2) as (a,b,c).
Step 3: Substitute into the Plane Equation
Substituting the values into the plane equation:
−14(x+10)+6(y−5)+2(z−4)=0
Step 4: Expand the Equation
Now, we expand the equation:
−14x−140+6y−30+2z−8=0
Combining the constant terms:
−14x+6y+2z−178=0
Step 5: Simplify the Equation
To simplify, we can divide the entire equation by 2:
−7x+3y+z−89=0
Rearranging gives us the final equation of the plane:
7x−3y−z+89=0
Final Answer
The equation of the plane is:
7x−3y−z+89=0
---
The direction ratios of the line can be found using the two points: (4,−1,2) and (−10,5,4).
The equation of a plane can be expressed in the form:
Substituting the values into the plane equation:
Now, we expand the equation:
To simplify, we can divide the entire equation by 2:
The equation of the plane is:
Topper's Solved these Questions
Similar Questions
If he line drawn from the point (−2,−1,−3) meets a plane at right angle at the point (1,−3,3), find the equation of the plane.
View SolutionIf the line drawn from the point (−2,−1,−3) meets a plane at right angle at the point (1,−3,3), find the equation of the plane.
View SolutionThe foot of the perpendicular drawn from the origin to the plane is the point (2, 5, 7). Find the equation of the plane.
View SolutionIn the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find :
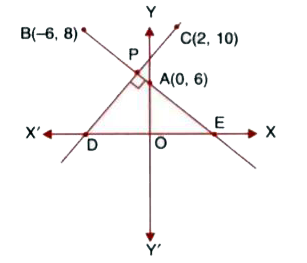
equation of line AB.
View SolutionIn the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find :
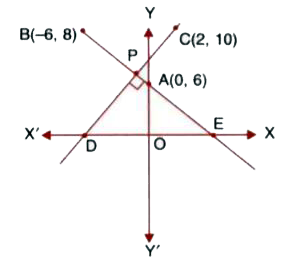
equation of line CD.
View SolutionThe foot of perpendicular drawn from the origin to the plane is (4,−2,−5). Find the equation of the plane.
View SolutionFind the equation of the plane passing through the points (0,-1,-1), (4,5,1) and (3,9,4). Also find the vector equation of the plane.
View SolutionIf a plane meets the equations axes at A,BandC such that the centroid of the triangle is (1,2,4), then find the equation of the plane.
View SolutionIf a plane meets the equations axes at A,BandC such that the centroid of the triangle is (1,2,4), then find the equation of the plane.
View SolutionThe coordinate of the foot of the perpendicular drawn from the origin to a plane are (12, -4, 3). Find the equation of the plane.
View Solution
