Given 4725=3a5b7c, find the integral values of a, b and c the value of 2−a3b7c
To solve the problem, we need to find the integral values of a, b, and c in the equation 4725=3a⋅5b⋅7c and then calculate the value of 2−a⋅3b⋅7c.
Step 1: Factor 4725 into its prime factors
We start by dividing 4725 by the smallest prime numbers until we reach 1.
1. Divide by 3:
- 4725÷3=1575
- 1575÷3=525
- 525÷3=175
- 175 is not divisible by 3.
2. Divide by 5:
- 175÷5=35
- 35÷5=7
- 7 is a prime number.
So, we can express 4725 as:
4725=33⋅52⋅71
Step 2: Identify the values of a, b, and c
From the factorization, we can directly compare the powers of the prime factors:
- a=3
- b=2
- c=1
Step 3: Calculate 2−a⋅3b⋅7c
Now we substitute the values of a, b, and c into the expression 2−a⋅3b⋅7c:
2−a=2−3=123=18
3b=32=9
7c=71=7
Now, we can combine these:
2−a⋅3b⋅7c=18⋅9⋅7
Step 4: Simplify the expression
Calculating this step-by-step:
1. First calculate 9⋅7=63.
2. Then multiply by 18:
638
Final Answer
Thus, the integral values are:
- a=3
- b=2
- c=1
And the value of 2−a⋅3b⋅7c is:
638
---
We start by dividing 4725 by the smallest prime numbers until we reach 1.
- 4725÷3=1575
- 1575÷3=525
- 525÷3=175
- 175 is not divisible by 3.
- 175÷5=35
- 35÷5=7
- 7 is a prime number.
4725=33⋅52⋅71
From the factorization, we can directly compare the powers of the prime factors:
- a=3
- b=2
- c=1
Now we substitute the values of a, b, and c into the expression 2−a⋅3b⋅7c:
2−a=2−3=123=18
3b=32=9
7c=71=7
2−a⋅3b⋅7c=18⋅9⋅7
Calculating this step-by-step:
1. First calculate 9⋅7=63.
2. Then multiply by 18:
638
Thus, the integral values are:
- a=3
- b=2
- c=1
638
Topper's Solved these Questions
Similar Questions
Knowledge Check
If 7c−2b=15and3b−6c=2, what is the value of b+c ?
A−27B−3C8D17
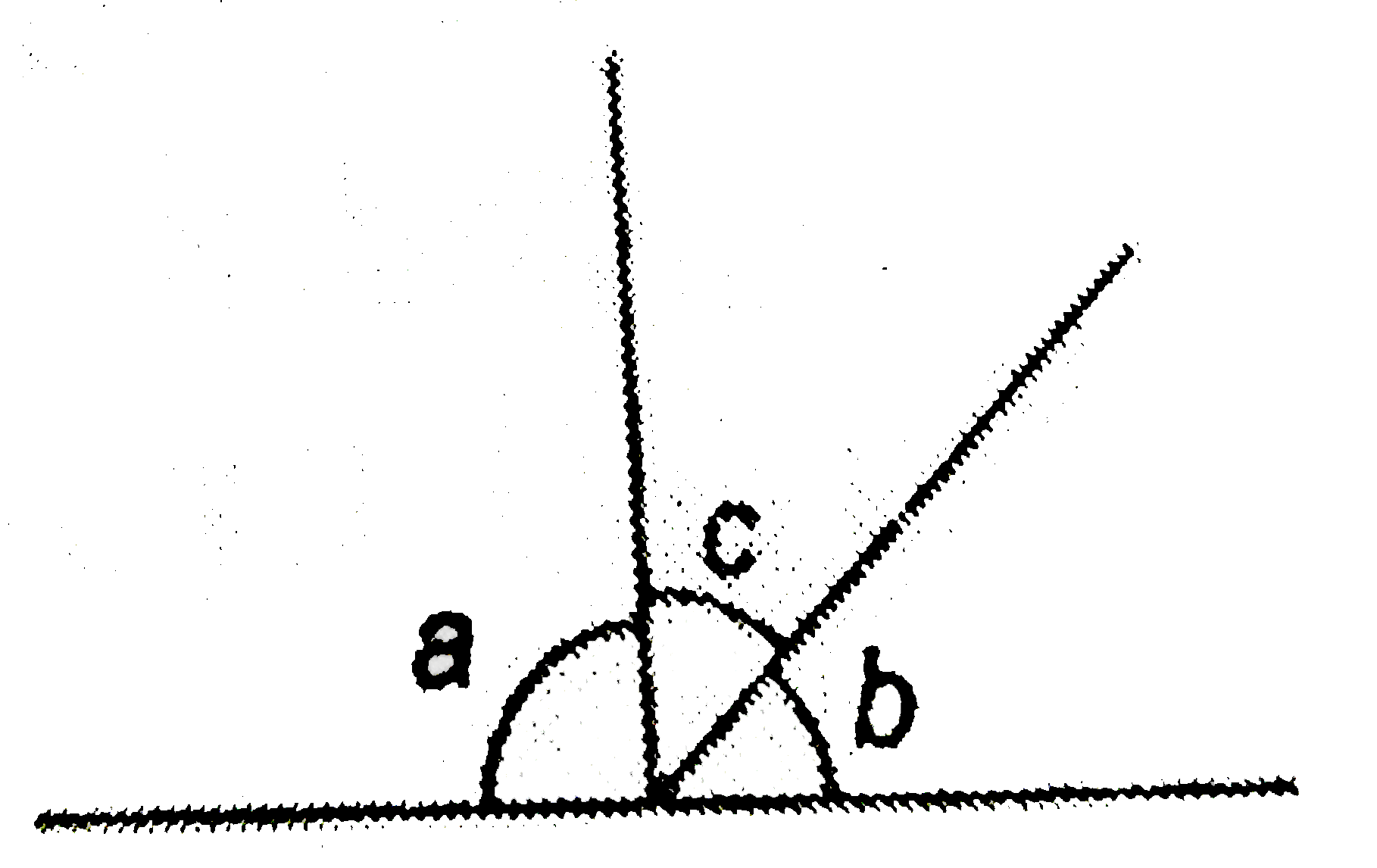
In the given figure if c=3b and a=5b find the value of a and b
View SolutionIf a=2,b≡3andc=5, then find the value of a3+b3+c3.
View SolutionIf a=2,b≡3andc=5, then find the value of a3+b3+c3.
View SolutionIf 49392=a4b2c3, find the value of a, b and c , where a, b and c are different positive primes.
View SolutionIf 7c+8b=15and3b−c=2, what is the value of b ?
View SolutionIf 1176=2a× 3b× 7c, and a,b and c are natural numbers. find a,b,c.
View SolutionIf a+b+c=6 and ab+bc+ca=11 , find the value of a3+b3+c3−3abc
View Solution
