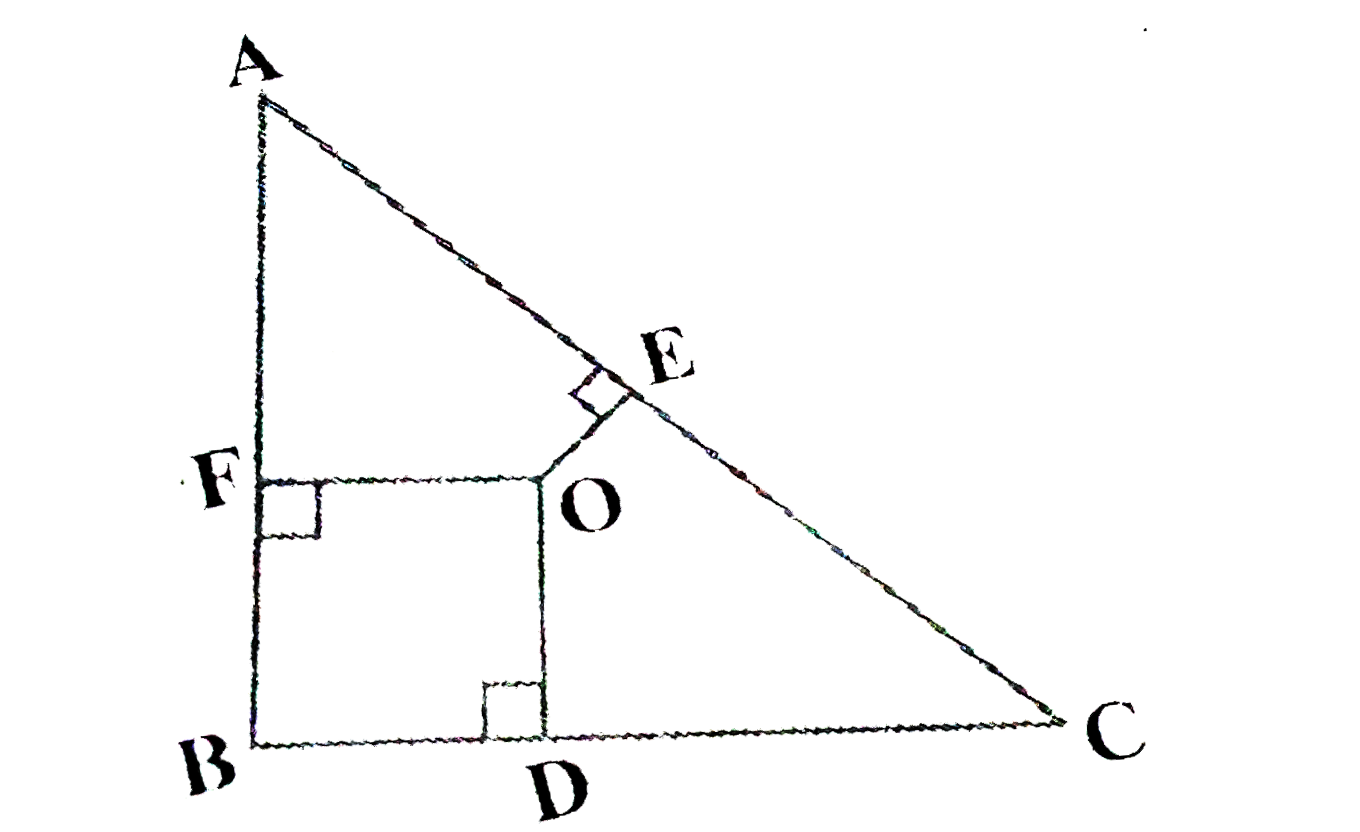
From a point $O$ in the interior of a $A B C$ , perpendiculars $O D, O E$ and $O F$ are drawn to the sides $B C, C A$ and $A B$ respectively. Prove that: (i) $A F^{2} + B D^{2} + C E^{2} = O A^{2} + O B^{2} + O C^{2} - O D^{2} - O E^{2} - O F^{2}$ (ii) $A F^{2} + B D^{2} + C E^{2} = A E^{2} + C D^{2} + B F^{2}$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we will prove the two statements step by step.
Given:
- A triangle $A B C$
- A point $O$ inside triangle $A B C$
- Perpendiculars $O D, O E, O F$ are drawn from point $O$ to the sides $B C, C A, A B$ respectively.
To Prove:
1. $A F^{2} + B D^{2} + C E^{2} = O A^{2} + O B^{2} + O C^{2} - O D^{2} - O E^{2} - O F^{2}$
2. $A F^{2} + B D^{2} + C E^{2} = A E^{2} + C D^{2} + B F^{2}$
Proof:
Part (i):
1. Apply Pythagorean Theorem:
- In triangle $O A F$ :
$O A^{2} = A F^{2} + O F^{2} (1)$
- In triangle $O B D$ :
$O B^{2} = B D^{2} + O D^{2} (2)$
- In triangle $O E C$ :
$O C^{2} = C E^{2} + O E^{2} (3)$
2. Add equations (1), (2), and (3):
$O A^{2} + O B^{2} + O C^{2} = (A F^{2} + O F^{2}) + (B D^{2} + O D^{2}) + (C E^{2} + O E^{2})$
$O A^{2} + O B^{2} + O C^{2} = A F^{2} + B D^{2} + C E^{2} + O F^{2} + O D^{2} + O E^{2}$
3. Rearranging the equation:
$A F^{2} + B D^{2} + C E^{2} = O A^{2} + O B^{2} + O C^{2} - O D^{2} - O E^{2} - O F^{2}$
Thus, we have proved the first part.
Part (ii):
1. Apply Pythagorean Theorem in different triangles:
- For triangle $O B D$ :
$O B^{2} = O D^{2} + B D^{2} (4)$
- For triangle $O E C$ :
$O C^{2} = O E^{2} + C E^{2} (5)$
- For triangle $O A F$ :
$O A^{2} = O F^{2} + A F^{2} (6)$
2. Subtract equations (4), (5), and (6):
- From (4) and (5):
$O B^{2} - O C^{2} = (O D^{2} + B D^{2}) - (O E^{2} + C E^{2})$
- From (5) and (6):
$O C^{2} - O A^{2} = (O E^{2} + C E^{2}) - (O F^{2} + A F^{2})$
- From (6) and (4):
$O A^{2} - O B^{2} = (O F^{2} + A F^{2}) - (O D^{2} + B D^{2})$
3. Adding these equations:
$(O B^{2} - O C^{2}) + (O C^{2} - O A^{2}) + (O A^{2} - O B^{2}) = (B D^{2} - C E^{2}) + (C E^{2} - A F^{2}) + (A F^{2} - B D^{2})$
- The left-hand side cancels out:
$0 = B D^{2} - C E^{2} + C E^{2} - A F^{2} + A F^{2} - B D^{2}$
- Rearranging gives:
$A F^{2} + C E^{2} = A E^{2} + C D^{2} + B F^{2}$
Thus, we have proved the second part.
Final Result:
1. $A F^{2} + B D^{2} + C E^{2} = O A^{2} + O B^{2} + O C^{2} - O D^{2} - O E^{2} - O F^{2}$
2. $A F^{2} + B D^{2} + C E^{2} = A E^{2} + C D^{2} + B F^{2}$

|

Updated on:7/8/2024

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

RD SHARMA ENGLISH-TRIANGLES-All Questions

Home
Ask Doubt
Profile