In Fig. 4.245, RSDBPQ . If CP=PD=11cm and DR=RA=3cm . Then the values of x and y are respectively (FIGURE) 12, 10 (b) 14, 6 (c) 10, 7 (d) 16, 8
To solve the problem, we need to find the values of x and y in the triangles RSD and BPQ given the lengths CP=PD=11cm and DR=RA=3cm.
1. Identify the Triangles: We have two triangles, △ASR and △ABD, where RS is parallel to BD. This parallelism allows us to use the properties of similar triangles.
2. Use the Properties of Similar Triangles: Since RS∥BD, we can say that the triangles △ASR and △ABD are similar by the AA (Angle-Angle) criterion. This means that the corresponding angles are equal.
3. Set Up the Ratios: From the properties of similar triangles, we can set up the following ratio of corresponding sides:
ARAB=SRBD=ASAD
4. Substitute Known Values: We know:
- AR=3cm
- AD=AR+RD=3+3=6cm
- Let SR=y and BD=x.
Thus, we can write:
36=yx
5. Simplify the Ratio: The ratio 36 simplifies to 12. Therefore, we have:
yx=12
6. Express y in terms of x: From the ratio, we can express y as:
y=12x
7. Check the Options: We need to find values of x and y from the given options:
- (a) 12,10
- (b) 14,6
- (c) 10,7
- (d) 16,8
8. Substitute Values: We can substitute the values of x from the options into y=12x:
- For x=12: y=12×12=6 (not an option)
- For x=14: y=12×14=7 (not an option)
- For x=10: y=12×10=5 (not an option)
- For x=16: y=12×16=8 (this is an option)
9. Conclusion: The correct values of x and y are 16 and 8 respectively.
Final Answer:
The values of x and y are 16 and 8 respectively.
ARAB=SRBD=ASAD
- AR=3cm
- AD=AR+RD=3+3=6cm
- Let SR=y and BD=x.
36=yx
yx=12
y=12x
- (a) 12,10
- (b) 14,6
- (c) 10,7
- (d) 16,8
- For x=12: y=12×12=6 (not an option)
- For x=14: y=12×14=7 (not an option)
- For x=10: y=12×10=5 (not an option)
- For x=16: y=12×16=8 (this is an option)
The values of x and y are 16 and 8 respectively.
Topper's Solved these Questions
Similar Questions
In Fig. 4.144, we have AB∥CD∥EF . If AB=6cm , CD=x cm , EF=10cm , BD=4cm and DE=y cm , calculate the values of x and y . (FIGURE)
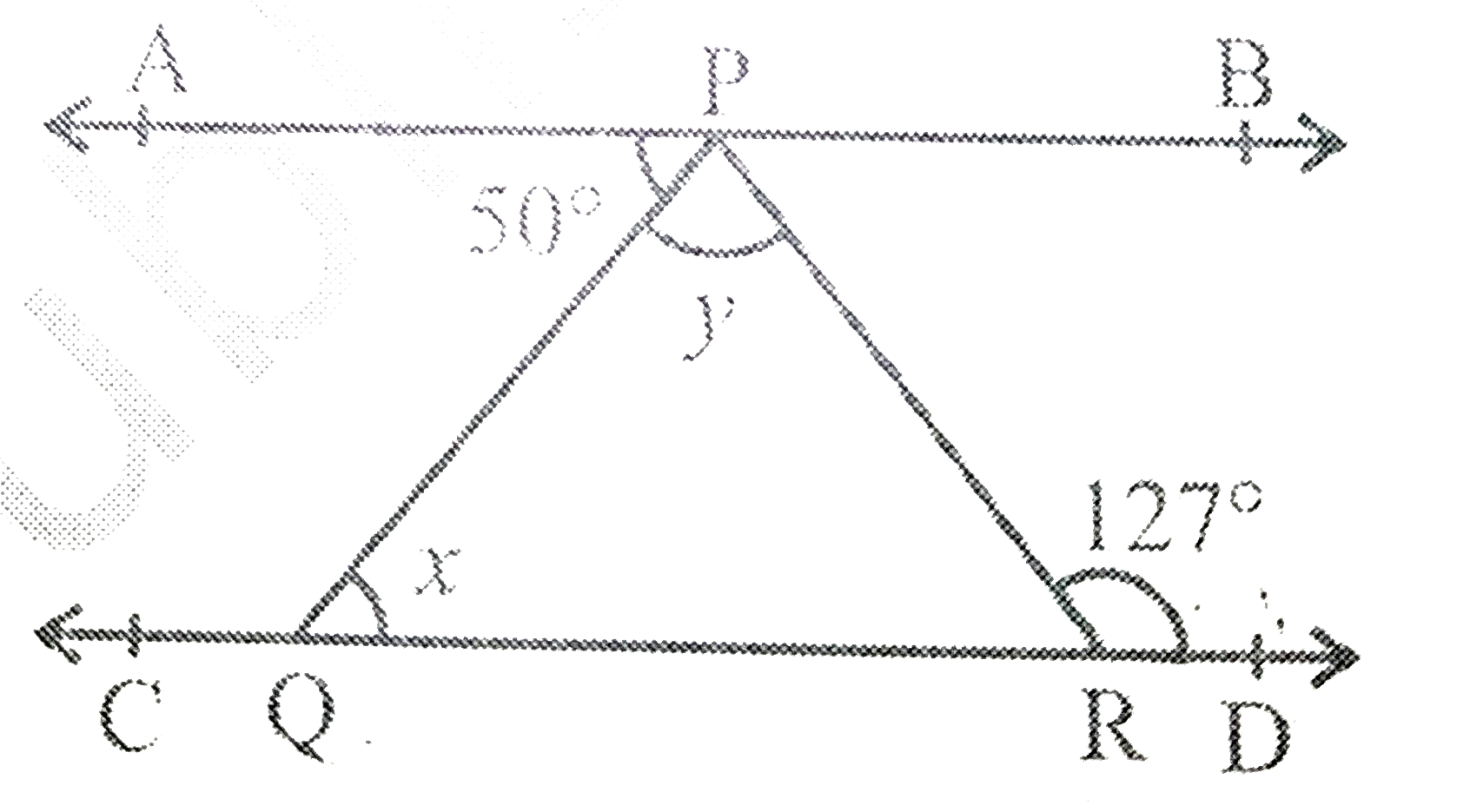
View SolutionIn Fig. 6.32, if AB∣∣CD,∠APQ=50∘and∠PRD=127∘, find x and y.
View SolutionIn Fig. 4.42, AD is the bisector of ∠BAC . If AB=10cm . AC=14cm and BC=6cm , find BD and DC . (FIGURE)
View SolutionIn PQR , right-angled at Q, PQ=3cm and PR=6cm . Determine ∠P and ∠R .
View SolutionIn Fig. 4.177, ACB∼APQ . If BC=10cm, PQ=5cm, BA=6.5cm and AP=2.8cm find CA and AQ . Also, find the area (ACB):area (APQ) . (FIGURE)
View SolutionIn Fig.38, ABCD and PQRC are square such that AD=22 cm and PC=y cm. If the area of the shaded region is 403 cm2, then the value of y is (a)3 (b) 6 (c)9 (d) 10
View SolutionIn Fig. 10.97, the sides AB, BC and CA of triangle ABC , touch a circle at P, Q and R respectively. If PA=4cm , BP=3cm and AC=11cm , then length of BC is (FIGURE) (a) 11cm (b) 10cm (c) 14cm (d) 15cm
View SolutionIn △PQR , right-angled at Q, PQ=3cm and PR=6cm . Determine ∠P and ∠R .
View SolutionIn Fig.9.29, ar (BDP) = ar (ARC)and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
View SolutionIn Figure, AD ⊥CD and CB ⊥CD If AQ=BP and DP=CQ, prove that ∠DAQ=∠CBP.
View Solution
