How many pairs of adjacent angles are formed when two lines intersect at a point?
To determine how many pairs of adjacent angles are formed when two lines intersect at a point, we can follow these steps:
1. Understanding the Intersection of Lines:
- When two lines intersect, they meet at a single point. Let's label this point as point O.
2. Drawing the Lines:
- Draw two lines that intersect at point O. Label the lines as line AB and line CD.
3. Identifying the Angles:
- The intersection of lines AB and CD creates four angles around point O. Let's label these angles as ∠1, ∠2, ∠3, and ∠4.
4. Identifying Adjacent Angles:
- Adjacent angles are angles that share a common side and a common vertex.
- In our case:
- ∠1 and ∠2 are adjacent (they share side OB and vertex O).
- ∠2 and ∠4 are adjacent (they share side OD and vertex O).
- ∠4 and ∠3 are adjacent (they share side OC and vertex O).
- ∠3 and ∠1 are adjacent (they share side OA and vertex O).
5. Counting the Pairs of Adjacent Angles:
- From the above, we can see that there are four pairs of adjacent angles:
- (∠1, ∠2)
- (∠2, ∠4)
- (∠4, ∠3)
- (∠3, ∠1)
6. Conclusion:
- Therefore, when two lines intersect at a point, they form 4 pairs of adjacent angles.
Final Answer:
4 pairs of adjacent angles are formed when two lines intersect at a point.
- When two lines intersect, they meet at a single point. Let's label this point as point O.
- Draw two lines that intersect at point O. Label the lines as line AB and line CD.
- The intersection of lines AB and CD creates four angles around point O. Let's label these angles as ∠1, ∠2, ∠3, and ∠4.
- Adjacent angles are angles that share a common side and a common vertex.
- In our case:
- ∠1 and ∠2 are adjacent (they share side OB and vertex O).
- ∠2 and ∠4 are adjacent (they share side OD and vertex O).
- ∠4 and ∠3 are adjacent (they share side OC and vertex O).
- ∠3 and ∠1 are adjacent (they share side OA and vertex O).
- From the above, we can see that there are four pairs of adjacent angles:
- (∠1, ∠2)
- (∠2, ∠4)
- (∠4, ∠3)
- (∠3, ∠1)
- Therefore, when two lines intersect at a point, they form 4 pairs of adjacent angles.
4 pairs of adjacent angles are formed when two lines intersect at a point.
Topper's Solved these Questions
Similar Questions
How many pairs of adjacent angles are formed when two lines intersect in a point?
View SolutionWrite five pairs of adjacent angles.
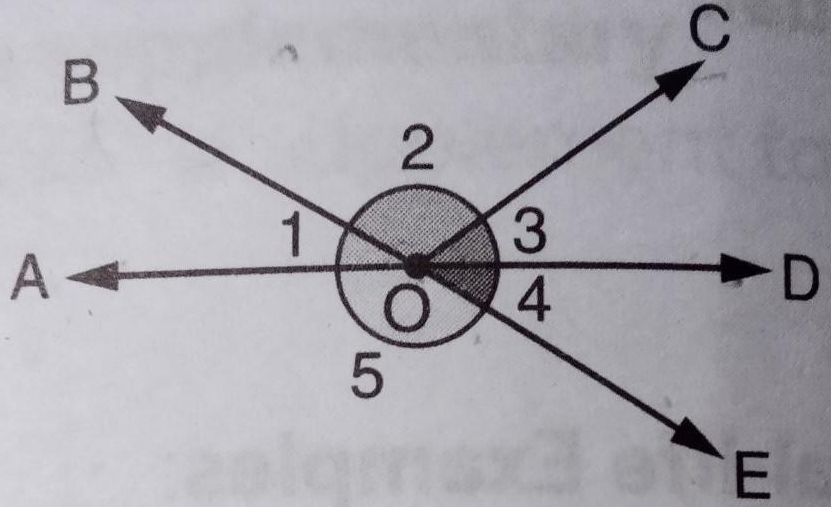
View SolutionHow many pairs of adjacent angles, in all, can you name in Figure.
View SolutionHow many pairs of adjacent angles, in all, can you name in Figure?

View SolutionIn Figure, ABCD is a quadrilateral. Name a pair of adjacent sides. Name a pair of opposite sides. How many pairs of adjacent sides are there? How many pairs of opposite sides are there? Name a pair of adjacent angles. Name a pair of opposite angles. How many pairs of adjacent angles are there? How many pairs of opposite angles are there?
View SolutionIn Figure, write all pairs of adjacent angles and all the linear pairs.
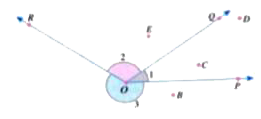
View SolutionAnswer the following from the figure given alongside.
 .
.
a. Name ∠POQ in two more ways.
b. Name all the pairs of adjacent angles.
c. Name the points in the interior of ∠1.
d. Name the points in the exterior of ∠1.
e. Name the points on ∠1.
View SolutionIn parallelogram ABCD, the bisectors of adjacent angles A and D intersect each other at point P. prove that ∠APD=90∘.
View SolutionHow many angles are formed in the figures. Name them.
View SolutionFill in the blanks:(i) If two angles are complementary, then the sum of their measures is _______.(ii) If two angles are supplementary, then the sum of their measures is ______.(iii) Two angles forming a linear pair are _______________.(iv) If two adjacent angles are supplementary, they form a ___________.(v) If two lines intersect at a point, then the vertically opposite angles are always_____________.(vi) If two lines intersect at a point, and if one pair of vertically opposite angles areacute angles, then the other pair of vertically opposite angles are __________.
View Solution
