Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No of accident (x) 0 1 2 3 4 5 Total Frequency (f): 46 ? ? 25 10 5 200
To find the missing frequencies in the given frequency distribution, we will follow these steps:
Step 1: Set up the frequency distribution table
We have the number of accidents (x) and their corresponding frequencies (f). The table is as follows:
| No of accidents (x) | Frequency (f) |
|----------------------|---------------|
| 0 | 46 |
| 1 | ? (let's call it x) |
| 2 | ? (let's call it y) |
| 3 | 25 |
| 4 | 10 |
| 5 | 5 |
| Total | 200 |
Step 2: Write down the known values
We know:
- The total frequency (∑f) = 200
- The mean (μ) = 1.46
Step 3: Calculate the sum of frequencies
The sum of frequencies can be expressed as:
Total frequency=46+x+y+25+10+5
This simplifies to:
86+x+y=200
From this, we can derive our first equation:
x+y=200−86
x+y=114 (Equation 1)
Step 4: Calculate the sum of xi * fi
Next, we calculate the sum of the product of the number of accidents and their frequencies:
∑(xi⋅fi)=0⋅46+1⋅x+2⋅y+3⋅25+4⋅10+5⋅5
This simplifies to:
0+x+2y+75+40+25=x+2y+140
Thus, we can express the mean as:
Mean=∑(xi⋅fi)∑fi
Substituting the known values:
1.46=x+2y+140200
Step 5: Solve for x + 2y
Multiplying both sides by 200 gives:
1.46⋅200=x+2y+140
292=x+2y+140
Rearranging gives us our second equation:
x+2y=292−140
x+2y=152 (Equation 2)
Step 6: Solve the system of equations
Now we have two equations:
1. x+y=114 (Equation 1)
2. x+2y=152 (Equation 2)
We can solve these equations simultaneously. From Equation 1, we can express x in terms of y:
x=114−y
Substituting this into Equation 2:
(114−y)+2y=152
114+y=152
y=152−114
y=38
Step 7: Find x
Now substitute y=38 back into Equation 1:
x+38=114
x=114−38
x=76
Conclusion
The missing frequencies are:
- For 1 accident: x=76
- For 2 accidents: y=38
Thus, the final missing frequencies are 76 and 38.
We have the number of accidents (x) and their corresponding frequencies (f). The table is as follows:
|----------------------|---------------|
| 0 | 46 |
| 1 | ? (let's call it x) |
| 2 | ? (let's call it y) |
| 3 | 25 |
| 4 | 10 |
| 5 | 5 |
| Total | 200 |
We know:
- The total frequency (∑f) = 200
- The mean (μ) = 1.46
The sum of frequencies can be expressed as:
Total frequency=46+x+y+25+10+5
This simplifies to:
86+x+y=200
From this, we can derive our first equation:
x+y=200−86
x+y=114 (Equation 1)
Next, we calculate the sum of the product of the number of accidents and their frequencies:
∑(xi⋅fi)=0⋅46+1⋅x+2⋅y+3⋅25+4⋅10+5⋅5
This simplifies to:
0+x+2y+75+40+25=x+2y+140
Thus, we can express the mean as:
Mean=∑(xi⋅fi)∑fi
Substituting the known values:
1.46=x+2y+140200
Multiplying both sides by 200 gives:
1.46⋅200=x+2y+140
292=x+2y+140
Rearranging gives us our second equation:
x+2y=292−140
x+2y=152 (Equation 2)
Now we have two equations:
1. x+y=114 (Equation 1)
2. x+2y=152 (Equation 2)
x=114−y
(114−y)+2y=152
114+y=152
y=152−114
y=38
Now substitute y=38 back into Equation 1:
x+38=114
x=114−38
x=76
The missing frequencies are:
- For 1 accident: x=76
- For 2 accidents: y=38
Topper's Solved these Questions
Similar Questions
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No. of accident (x), 0, 1 , 2 , 3, 4, 5 , Total Frequency is 200 and no. of days (f): 46 , ? , ? , 25 , 10 , 5
View SolutionFind the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50. x : 10 30 50 70 90 f : 17 f1 32 f2 19 Total 120.
View SolutionFind the mean for the following frequency distribution :
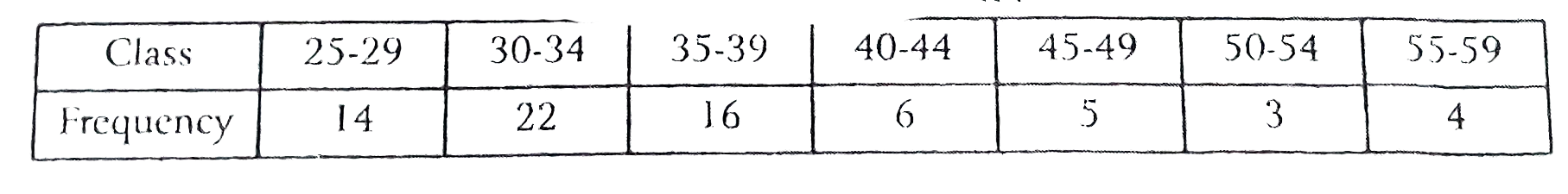
View SolutionFind the mean and variance for the following frequency distributions in
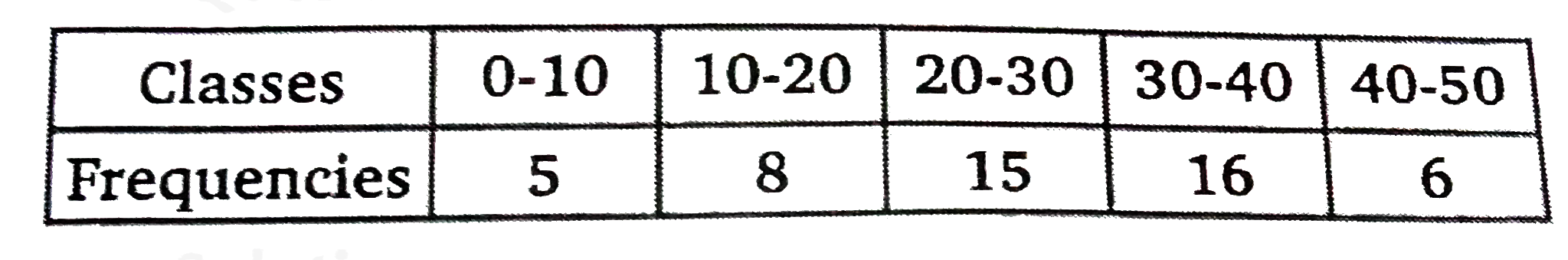
View SolutionFind the mean and variance for the following frequency distributions in
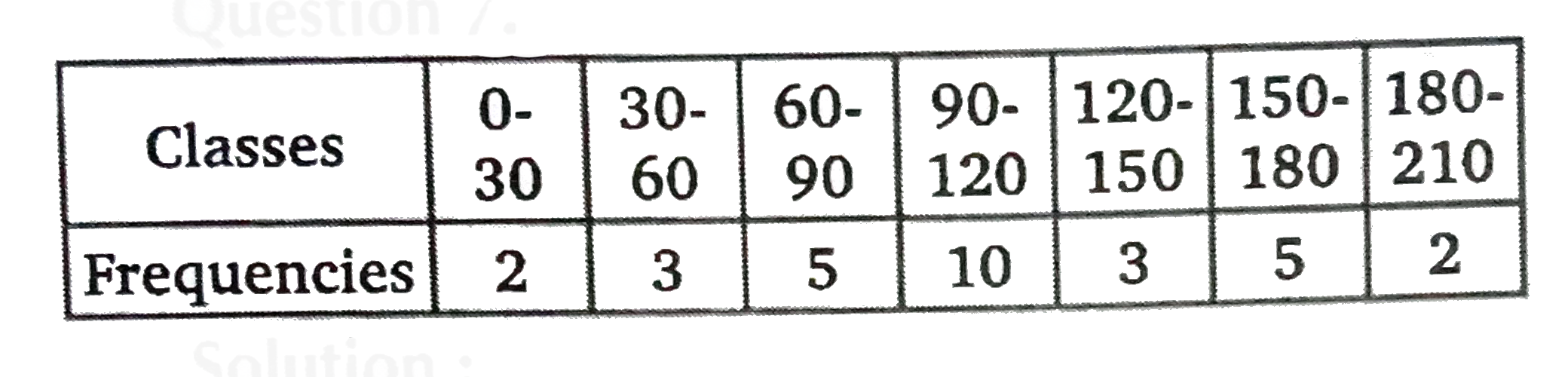
View SolutionFind the missing frequencies in the following distribution table. It is given that the mean of these distributions is 56 and their total is 90 i.e., ∑f=90

View SolutionFind the mean of the following frequency distribution by direct method.

View SolutionFind the mean and standard deviation of the following frequency distribution :

View SolutionFind the mean deviation from the median for following frequency distribution :

View SolutionThe mean of the following frequency distribution is 2117. Find the value of f

View Solution