Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45o
To construct a pair of tangents to a circle of radius 4.5 cm that are inclined to each other at an angle of 45 degrees, follow these steps:
1. Draw the Circle:
- Using a compass, draw a circle with a radius of 4.5 cm. Label the center of the circle as O.
Hint: Ensure your compass is set to exactly 4.5 cm before drawing the circle.
2. Mark Point A on the Circle:
- Choose any point on the circumference of the circle and label it as A.
Hint: You can pick any point on the circle; it doesn't have to be at the top or bottom.
3. Construct Point B:
- To find point B, you need to create an angle of 135 degrees at point O (the center of the circle) between line OA and line OB. Use a protractor to measure and mark point B on the circumference such that the angle AOB is 135 degrees.
Hint: Remember that the angle between the tangents will be 45 degrees, so the angle at the center must be 180° - 45° = 135°.
4. Draw Tangents from Points A and B:
- To draw the tangent from point A:
- Place the compass point at A and draw an arc that intersects the circle at two points. Label these intersection points as C and D.
- With the same radius, place the compass point at C and draw an arc above the line OA. Then, without changing the compass width, place the compass point at D and draw another arc that intersects the first arc. Label the intersection point as E.
- Draw a straight line from A to E. This line AE is the tangent from point A.
Hint: Ensure the arcs are drawn carefully to find the intersection point accurately.
5. Repeat for Point B:
- Repeat the same process to draw the tangent from point B:
- Draw arcs from point B that intersect the circle at two points (F and G).
- Use the same method to find the intersection point H above line OB, and draw the tangent line BH.
Hint: Follow the same steps as you did for point A to maintain consistency.
6. Label the Tangents:
- You should now have two tangent lines, AE and BH, which intersect at an angle of 45 degrees.
Hint: Ensure that the tangents do not cross the circle; they should only touch it at points A and B.
Final Check:
- Verify that the angle between the two tangents is indeed 45 degrees by using a protractor.
- Using a compass, draw a circle with a radius of 4.5 cm. Label the center of the circle as O.
- Choose any point on the circumference of the circle and label it as A.
- To find point B, you need to create an angle of 135 degrees at point O (the center of the circle) between line OA and line OB. Use a protractor to measure and mark point B on the circumference such that the angle AOB is 135 degrees.
- To draw the tangent from point A:
- Place the compass point at A and draw an arc that intersects the circle at two points. Label these intersection points as C and D.
- With the same radius, place the compass point at C and draw an arc above the line OA. Then, without changing the compass width, place the compass point at D and draw another arc that intersects the first arc. Label the intersection point as E.
- Draw a straight line from A to E. This line AE is the tangent from point A.
- Repeat the same process to draw the tangent from point B:
- Draw arcs from point B that intersect the circle at two points (F and G).
- Use the same method to find the intersection point H above line OB, and draw the tangent line BH.
- You should now have two tangent lines, AE and BH, which intersect at an angle of 45 degrees.
- Verify that the angle between the two tangents is indeed 45 degrees by using a protractor.
Topper's Solved these Questions
Similar Questions
Draw a pair of tangents to a circle of radius 5cm which are inclined to each other at an angle of 60o .
View SolutionDraw a pair of tangent to a circle of radius 5 cm which are inclined to each other at an angle of 60∘. Give steps of construction.
View SolutionDraw a pair of tangent to a circle of radius 5 cm which are inclined to each other at an angle of 60∘. Give steps of construction.
View SolutionConstruct a pair of tangents to a circle of radius 3 cm which are inclined to each other at an angle of 60∘
View SolutionTo draw a pair of tangents to a circle which are inclined to each other at an angle of 60∘, it is required to draw tangents at end points of those two radii of the circle, the angle between them should be
View SolutionTo draw a pair of tangents to a circle which are inclined to each other at an angle of 1000, it is required to draw tangents at end points of those two radii of the circle, the angle between which should be: 1000 (b) 500 (c) 800 (d) 2000
View SolutionDraw a circle of radius 4 cm. Draw pair of tangents to this circle which are inclined to each other at 75∘.
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80o then ∠POA is equal to :
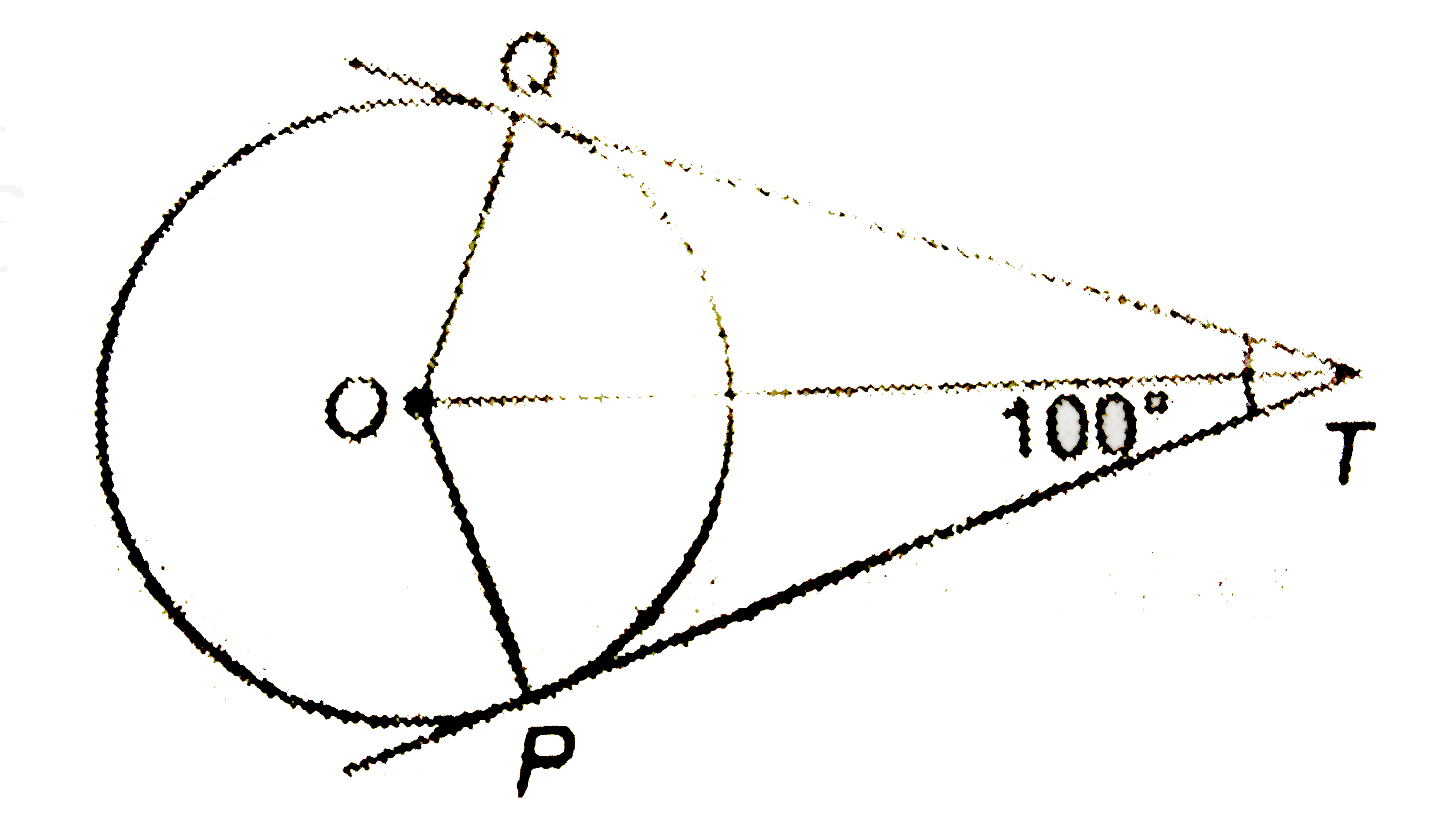
View SolutionTwo tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in figure. If they are inclined to each other at an angle of 100∘, then what is the value of ∠POQ?
View SolutionThe diagonals of a parallelogram are inclined to each other at an angle of 45∘, while its sides aandb(a>0) are inclined to each other at an angle of 30∘, then the value of ab is
View Solution
