A parachutist is descending vertically and makes angles of elevation of 45∘ and 60∘ at two observing points 100m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground from the just observation point.
To solve the problem step-by-step, we will follow the information provided in the video transcript and derive the necessary equations to find the maximum height from which the parachutist falls and the distance of the point where he falls on the ground from the observation point.
Step 1: Draw the Diagram
1. Draw a vertical line representing the descent of the parachutist.
2. Mark point A as the starting point of the parachutist and point B as the point where he is currently located.
3. Mark points C and D as the two observation points, which are 100 meters apart on the left side of the parachutist.
4. Label the angles of elevation from points C and D to point B as 60° and 45°, respectively.
Step 2: Define Variables
- Let H be the height from which the parachutist falls (AB).
- Let X be the horizontal distance from point B to point C (BC).
- The distance between the two observation points (CD) is given as 100 meters.
Step 3: Use Trigonometry in Triangle ABC
Using triangle ABC, where angle C is 60°:
- The tangent of angle 60° is given by:
tan(60∘)=ABBC=HX
- Since tan(60∘)=√3, we have:
√3=HX⟹H=X√3(Equation 1)
Step 4: Use Trigonometry in Triangle ABD
Using triangle ABD, where angle D is 45°:
- The tangent of angle 45° is given by:
tan(45∘)=ABBD=HBD
- The base BD can be expressed as BC+CD=X+100:
1=HX+100⟹H=X+100(Equation 2)
Step 5: Set Equations Equal
Now, we have two equations for H:
1. H=X√3
2. H=X+100
Setting these equal to each other:
X√3=X+100
Step 6: Solve for X
Rearranging the equation gives:
X√3−X=100
X(√3−1)=100
X=100√3−1
Step 7: Rationalize the Denominator
To simplify X:
X=100(√3+1)(√3−1)(√3+1)=100(√3+1)3−1=100(√3+1)2=50(√3+1)
Calculating this gives approximately:
X≈50(1.732+1)≈50×2.732≈136.6 meters
Step 8: Calculate H
Now, substituting X back into Equation 1 to find H:
H=X√3=136.6×√3≈136.6×1.732≈236.6 meters
Final Answers
- The maximum height H from which the parachutist falls is approximately 236.6 meters.
- The distance X from the observation point to the point where he falls is approximately 136.6 meters.
1. Draw a vertical line representing the descent of the parachutist.
2. Mark point A as the starting point of the parachutist and point B as the point where he is currently located.
3. Mark points C and D as the two observation points, which are 100 meters apart on the left side of the parachutist.
4. Label the angles of elevation from points C and D to point B as 60° and 45°, respectively.
- Let H be the height from which the parachutist falls (AB).
- Let X be the horizontal distance from point B to point C (BC).
- The distance between the two observation points (CD) is given as 100 meters.
Using triangle ABC, where angle C is 60°:
- The tangent of angle 60° is given by:
tan(60∘)=ABBC=HX
- Since tan(60∘)=√3, we have:
√3=HX⟹H=X√3(Equation 1)
Using triangle ABD, where angle D is 45°:
- The tangent of angle 45° is given by:
tan(45∘)=ABBD=HBD
- The base BD can be expressed as BC+CD=X+100:
1=HX+100⟹H=X+100(Equation 2)
Now, we have two equations for H:
1. H=X√3
2. H=X+100
X√3=X+100
Rearranging the equation gives:
X√3−X=100
X(√3−1)=100
X=100√3−1
To simplify X:
X=100(√3+1)(√3−1)(√3+1)=100(√3+1)3−1=100(√3+1)2=50(√3+1)
Calculating this gives approximately:
X≈50(1.732+1)≈50×2.732≈136.6 meters
Now, substituting X back into Equation 1 to find H:
H=X√3=136.6×√3≈136.6×1.732≈236.6 meters
- The maximum height H from which the parachutist falls is approximately 236.6 meters.
- The distance X from the observation point to the point where he falls is approximately 136.6 meters.
Topper's Solved these Questions
Similar Questions
The angle of elevation of the top of a tower from a point 40 m away from its foot is 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower is 30∘ . Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower, is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 40 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground is 60∘. which is 25 m away from the foot of the tower. Find the height of the tower
View SolutionThe angle of elevation of the top of a tower a point A due south of it is 30∘ and from a point B due west of it is 45∘ .If the height of the tower is 100 meters ,then find the distance AB.
View SolutionIn figure , the angle of elevation of the top of a tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m, Find the distance of the point from the foot of the power .

View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
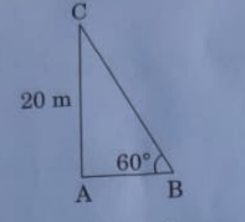
View Solution
