In the Fig. 13.12, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of JAB ? (FIGURE)
Step by step video & image solution for In the Fig. 13.12, J K L M is a square with sides of length 6 units. Points A and B are the mid-points of sides K L and L M respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of J A B ? (FIGURE) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the given figure, A, B, C and D are centres of four circles that have a radius of 1 unit. If a point is selected at random from interior of square ABCD, then what is the probability that it lies in the shaded region
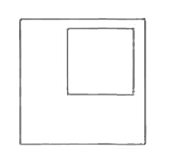
View SolutionIn the figure, the smaller square has sides of length 2 and the larger square has sides of length 4. If a point is chosen at random from the larger square, what is the probability that it will be from the small square?
View SolutionL and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.

View SolutionThe lengths of the tangents from the points A and B to a circle are l1 and l2 respectively. If points are conjugate with respect to the circle, then AB2=
View SolutionIn a convex polygon of 6 sides two diagonals are selected at random. The probability that they interesect at an interior point of the polygon is
View SolutionIn triangle LMN, bisector of interior angles at L and N intersect each other at point A. Prove that :
point A is equidistant from all the three sides of the triangle.
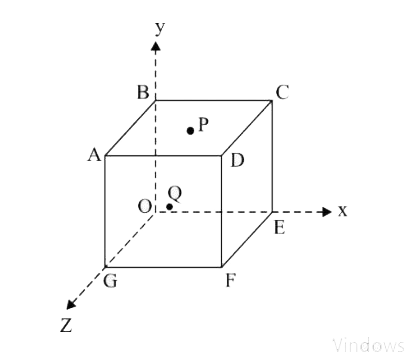
View SolutionIn the cube of side ‘l’ shown in the figure, the vector from the central point of face ABCD to the central point of the face ADGF will be:
View SolutionThe area of square ABCD is 16 cm2. Find the area of the square joining the mid-point of the sides.
View Solution
