If P(E)=0.05
, then P(¬ E)=
(a)−0.05
(b) 0.5
(c) 0.9
(d) 0.95
To find the probability of the non-occurrence of an event given that the probability of occurrence P(E)=0.05, we can follow these steps:
1. Understanding Total Probability:
The total probability of all possible outcomes must equal 1. This includes both the occurrence of the event E and the non-occurrence of the event not E.
P(E)+P(not E)=1
2. Substituting the Given Probability:
We know that P(E)=0.05. We can substitute this value into the equation.
0.05+P(not E)=1
3. Isolating the Probability of Non-Occurrence:
To find P(not E), we need to isolate it on one side of the equation. We can do this by subtracting 0.05 from both sides.
P(not E)=1−0.05
4. Calculating the Result:
Now we can perform the subtraction.
P(not E)=0.95
5. Final Answer:
Therefore, the probability of the non-occurrence of the event is
P(not E)=0.95
Conclusion:
The correct option is (d) 0.95.
The total probability of all possible outcomes must equal 1. This includes both the occurrence of the event E and the non-occurrence of the event not E.
We know that P(E)=0.05. We can substitute this value into the equation.
To find P(not E), we need to isolate it on one side of the equation. We can do this by subtracting 0.05 from both sides.
Now we can perform the subtraction.
Therefore, the probability of the non-occurrence of the event is
The correct option is (d) 0.95.
Topper's Solved these Questions
Similar Questions
If P(E)=0.59, find P(not E).
View SolutionIf two events A and B are such that P(Ac)=0.3.P(B)=0.4andP(A∩Bc)=0.5,thenP(BA∪Bc)= (a)0.9 (b). 0.5 (c). 0.6 (d). 0.25
View SolutionIf P(E) = 0.34, find p(not E).
View SolutionA,B,C are three events for which P(A)=0.4,P(B)=0.6,P(C)=0.5,P(A∪B)=0.75,P(A∩C)=0.30 and P(A∩B∩C)=0.2, if P(A∪B∪C)≥0.75, then P(B∩C) can take values
(a)0.1 (b) 0.2 (c)0.3 (d)0.5
View Solution0.02×0.05=
(a) 0.1
(b) 0.01
(c) 0.001
(d) 0.0001
View SolutionIf P(A∪B)=0.8 and P(A∩B)=0.3, then P(A)+P(B)= a. 0.3 b. 0.5 c. 0.7 d. 0.9
View SolutionIf P(A)=0.3,P(A∩B)=0.2 and P(A/B)=0.4 then P(A∪B)= (A) 0.7 (B) 0.8 (C) 0.9 (D) 0.6
View SolutionIf ef(x)=10+x10−x,x∈(−10,10)andf(x)=kf(200x100+x2),then k= (a) 0.5 (b) 0.6 (c) 0.7 (d) 0.8
View SolutionIf P(E)=0.05, what is the probability of not E?
View SolutionThe potential the cell at 25∘C is
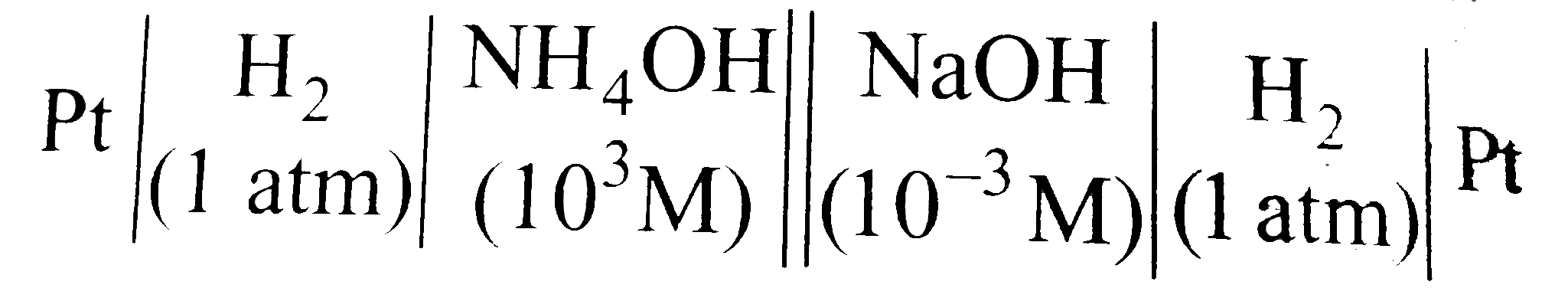
Given pKb of NH4OH=4.74
(a)0.05V
(b)−0.05V
(c)−0.28V
(d)0.28V
View Solution