In a circular table cover of radius 32cm, a design is formed leaving an equilateral triangle ABC as shown in figure. Find the area of shaded region.
To find the area of the shaded region on a circular table cover with a radius of 32 cm, where an equilateral triangle ABC is inscribed, we will follow these steps:
Step 1: Calculate the area of the circle
The formula for the area of a circle is given by:
Area of Circle=πr2
Here, the radius r=32 cm.
Substituting the value of r:
Area of Circle=π×(32)2=π×1024
Using π≈227:
Area of Circle=227×1024=225287 cm2
Step 2: Calculate the area of the equilateral triangle
For an equilateral triangle with side length a, the area can be calculated using the formula:
Area of Triangle=√34a2
To find the side length a of triangle ABC, we note that the triangle is inscribed in the circle. The relationship between the radius r of the circumcircle and the side length a of the equilateral triangle is given by:
a=r√3
Substituting r=32 cm:
a=32√3 cm
Now, substituting a into the area formula:
Area of Triangle=√34(32√3)2=√34×322×3=√34×1024×3=3072√34=768√3 cm2
Step 3: Calculate the area of the shaded region
The area of the shaded region is the area of the circle minus the area of the triangle:
Area of Shaded Region=Area of Circle−Area of Triangle
Substituting the values we calculated:
Area of Shaded Region=225287−768√3 cm2
Final Answer
Thus, the area of the shaded region is:
Area of Shaded Region=225287−768√3 cm2
The formula for the area of a circle is given by:
Area of Circle=πr2
Here, the radius r=32 cm.
Area of Circle=π×(32)2=π×1024
Using π≈227:
Area of Circle=227×1024=225287 cm2
For an equilateral triangle with side length a, the area can be calculated using the formula:
Area of Triangle=√34a2
To find the side length a of triangle ABC, we note that the triangle is inscribed in the circle. The relationship between the radius r of the circumcircle and the side length a of the equilateral triangle is given by:
a=r√3
Substituting r=32 cm:
a=32√3 cm
Now, substituting a into the area formula:
Area of Triangle=√34(32√3)2=√34×322×3=√34×1024×3=3072√34=768√3 cm2
The area of the shaded region is the area of the circle minus the area of the triangle:
Area of Shaded Region=Area of Circle−Area of Triangle
Substituting the values we calculated:
Area of Shaded Region=225287−768√3 cm2
Thus, the area of the shaded region is:
Area of Shaded Region=225287−768√3 cm2
Topper's Solved these Questions
Similar Questions
In a circular table cover of radius 32 cm, a design (shade) is formed leaving an equilateral traingle ABC in the middle as shown in the adjacent figure.Find the area of the shaded region.
View SolutionIn a circular table cover of radius 32 cm, a design (shade) is formed leaving an equilateral traingle ABC in the middle as shown in the adjacent figure.Find the area of the shaded region.
View Solution
Knowledge Check
In the joining figure , find the area of the shaded region.
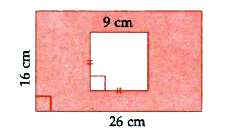 A325cm2B245cm2C335cm2D185cm2
A325cm2B245cm2C335cm2D185cm2
An equilateral triangle with side 12 is inscribed in a circle . Find the shaded area .A12π−36√3B36π−48√3C36π−36√3D48π−36√3
A girl formed of design in a circle of radius 42 cm leaving an equilateral triangle ABC in the middle as shown in the figure. Find the corvered area of the design. (Use √3=1.73andπ=227)

View SolutionFind the area of the shaded region in figure.

View SolutionFind the area of the shaded region in Figure.
View SolutionEach side of an equilateral triangle measure 10 cm. Find the area of the triangle .
View SolutionABC is an equilateral triangle inscribed in a circle of radius 4 cm. Find the area of the shaded portion.

View SolutionIn figure, find the area of the shaded region [Useπ=3.14]
View Solution
