A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is then the volume of the cylinder is (b) (c) (d)
To find the volume of the cylinder in which a sphere is inscribed, we can follow these steps:
1. Understand the Relationship Between the Sphere and Cylinder:
- The sphere touches the top, base, and lateral surface of the cylinder. This means that the diameter of the sphere is equal to the height of the cylinder, and the radius of the sphere is equal to the radius of the cylinder.
2. Define the Radius and Height:
- Let the radius of the sphere be r.
- Since the diameter of the sphere is 2r, the height of the cylinder (which is equal to the diameter of the sphere) is also 2r.
3. Volume Formula for a Cylinder:
- The volume V of a cylinder is given by the formula:
V=πr2h
where r is the radius of the base of the cylinder and h is the height of the cylinder.
4. Substitute the Values:
- We know that the radius of the cylinder is r and the height h is 2r. Substitute these values into the volume formula:
V=π(r2)(2r)
5. Simplify the Expression:
- Now simplify the expression:
V=2πr3
6. Conclusion:
- Therefore, the volume of the cylinder is:
V=2πr3
Final Answer
The volume of the cylinder is 2πr3, which corresponds to option (c).
---
- The sphere touches the top, base, and lateral surface of the cylinder. This means that the diameter of the sphere is equal to the height of the cylinder, and the radius of the sphere is equal to the radius of the cylinder.
- Let the radius of the sphere be r.
- Since the diameter of the sphere is 2r, the height of the cylinder (which is equal to the diameter of the sphere) is also 2r.
- The volume V of a cylinder is given by the formula:
V=πr2h
where r is the radius of the base of the cylinder and h is the height of the cylinder.
- We know that the radius of the cylinder is r and the height h is 2r. Substitute these values into the volume formula:
V=π(r2)(2r)
- Now simplify the expression:
V=2πr3
- Therefore, the volume of the cylinder is:
V=2πr3
The volume of the cylinder is 2πr3, which corresponds to option (c).
Topper's Solved these Questions
- SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDER CONEBOOK - RD SHARMA ENGLISHCHAPTER - SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDER CONEEXERCISE - All Questions
129 Videos
- TABULAR REPRESENTATION OF STATISTICAL DATA BOOK - RD SHARMA ENGLISHCHAPTER - TABULAR REPRESENTATION OF STATISTICAL DATA EXERCISE - All Questions
70 Videos
Similar Questions
The height h of cylinder equals the circumference of the cylinder. In terms of h, what is the volume of the cylinder? (a) h34π (b) h22π (c) h32 (d) πh3
View SolutionA right circular cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is (a) 3:5 (b) 2:5 (c) 3:1 (d) 1:3
View Solution
Knowledge Check

A cylinder whose base radius is 3 is inscribed in a sphere of radius 5. what is the difference between the volume of the sphere annd the volume of the cylinder?A88B297C354D448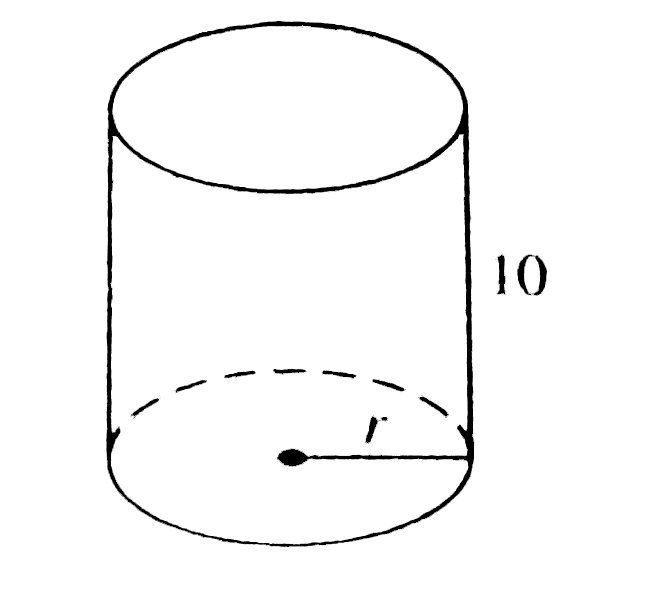
If the volume of the cylinder shown above is 1,000π3, then the value of r , the radius of the base , isAπB√10C10D10π
The height of a right circular cylinder of maxium volume inscribed in a sphere of radius 3 cm is
View SolutionThe largest sphere is cut off from a cube of side 6cm. The volume of the sphere will be 27π cm3 (b) 36π cm3 (c) 108π cm3 (d) 12π cm3
View SolutionIf r is the radius and h is height of the cylinder the volume will be (a) 13π2h (b) πr2h (c) 2πr (h+r) (d) 2πrh
View SolutionA cylinder has a surface area of 360π and height of 3. What is the diameter of the cylinder's circular base?
View SolutionIf the lateral surface of a cylinder is 94.2 cm2 and its heights is 5cm, find: [Use π=3.14] radius of its base (ii) volume of the cylinder
View SolutionFind the volume of the larges cylinder that can be inscribed in a sphere of radius r
View Solution
