If the mean of the following data is 15, find
To solve the problem step by step, we need to find the value of p given that the mean of the data is 15. The data consists of values xi and their corresponding frequencies fi.
Step 1: Write down the given data
We have the following values for xi and fi:
- xi=5,10,15,20,25
- fi=6,p,6,10,5
Step 2: Calculate xi×fi
We will calculate xi×fi for each xi:
- For x1=5 and f1=6:
x1×f1=5×6=30
- For x2=10 and f2=p:
x2×f2=10×p=10p
- For x3=15 and f3=6:
x3×f3=15×6=90
- For x4=20 and f4=10:
x4×f4=20×10=200
- For x5=25 and f5=5:
x5×f5=25×5=125
Step 3: Find the summation of fi and xi×fi
Now, we can find the total summation of fi and xi×fi:
- Summation of fi:
Σfi=6+p+6+10+5=27+p
- Summation of xi×fi:
Σ(xi×fi)=30+10p+90+200+125=445+10p
Step 4: Set up the equation for the mean
The formula for the mean ¯x is given by:
¯x=Σ(xi×fi)Σfi
Given that the mean is 15, we can set up the equation:
15=445+10p27+p
Step 5: Cross-multiply to solve for p
Cross-multiplying gives:
15(27+p)=445+10p
Expanding both sides:
405+15p=445+10p
Step 6: Rearrange the equation
Rearranging the equation:
405+15p−10p=445
405+5p=445
Subtracting 405 from both sides:
5p=445−405
5p=40
Step 7: Solve for p
Dividing both sides by 5:
p=405=8
Final Answer
Thus, the value of p is:
8
We have the following values for xi and fi:
- xi=5,10,15,20,25
- fi=6,p,6,10,5
We will calculate xi×fi for each xi:
- For x1=5 and f1=6:
x1×f1=5×6=30
- For x2=10 and f2=p:
x2×f2=10×p=10p
- For x3=15 and f3=6:
x3×f3=15×6=90
- For x4=20 and f4=10:
x4×f4=20×10=200
- For x5=25 and f5=5:
x5×f5=25×5=125
Now, we can find the total summation of fi and xi×fi:
- Summation of fi:
Σfi=6+p+6+10+5=27+p
- Summation of xi×fi:
Σ(xi×fi)=30+10p+90+200+125=445+10p
The formula for the mean ¯x is given by:
¯x=Σ(xi×fi)Σfi
Given that the mean is 15, we can set up the equation:
15=445+10p27+p
Cross-multiplying gives:
15(27+p)=445+10p
Expanding both sides:
405+15p=445+10p
Rearranging the equation:
405+15p−10p=445
405+5p=445
Subtracting 405 from both sides:
5p=445−405
5p=40
Dividing both sides by 5:
p=405=8
Thus, the value of p is:
8
Topper's Solved these Questions
Similar Questions
If the mean of the following data is 5.6, find p :

View SolutionFind the mean of the following data :

View SolutionFind the mean of the following data :

View SolutionFind the mean of the following data:
View SolutionIf the mean of the following data is 26, then find the value of p:
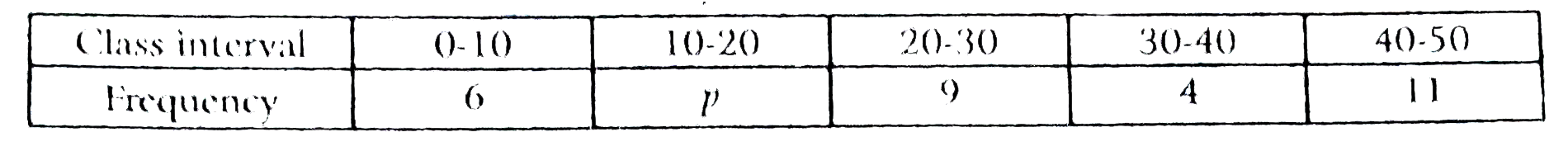
View SolutionIf the mean of the following data is 20.6. Find the value of p . x : 10 15 p 25 35 f : 3 10 25 7 5
View SolutionThe arithmetic mean of the following data is 25, find the value of k . xi : 5 15 25 35 45 fi : 3 k 3 6 2
View SolutionFind the mean for the following data
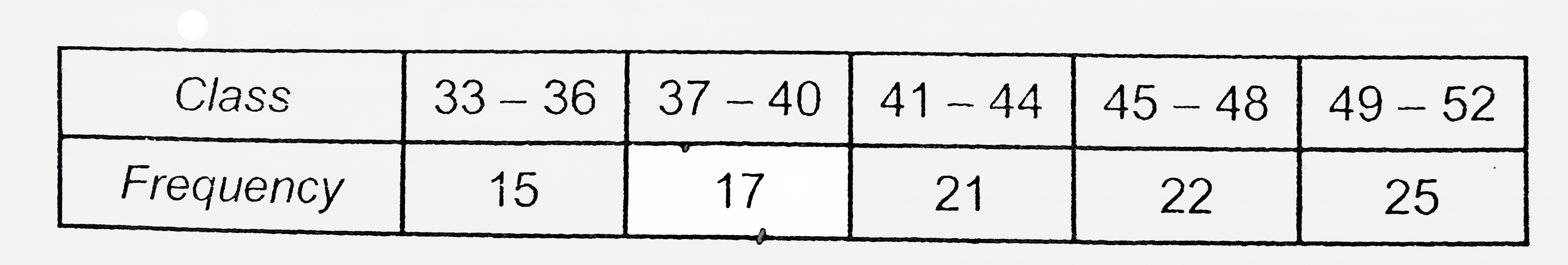
View SolutionIf the mean of the following data is 20.2, then find the value of p.

View SolutionFind the mean for the following data:

View Solution
