Let A={a,b,{c,d}, e} . Which of the following statements are false and why? (i) {a,b,e}∈A (ii) {a,b,c}⊂A (iii) φ∈A (iv) {φ}⊂A
To determine which statements about the set A={a,b,{c,d},e} are false, we will analyze each statement one by one.
1. Statement (i): {a,b,e}∈A
- The statement claims that the set {a,b,e} is an element of A.
- However, the elements of A are a, b, {c,d}, and e. The set {a,b,e} is not one of these elements; rather, it is a different set.
- Therefore, this statement is false.
2. Statement (ii): {a,b,c}⊂A
- This statement claims that the set {a,b,c} is a subset of A.
- For {a,b,c} to be a subset of A, all elements a, b, and c must be present in A.
- While a and b are present in A, c is not present as an individual element; instead, c is part of the nested set {c,d}.
- Therefore, this statement is false.
3. Statement (iii): φ∈A
- Here, φ represents the empty set.
- The statement claims that the empty set is an element of A.
- The elements of A are a, b, {c,d}, and e, and the empty set is not listed as one of the elements.
- Therefore, this statement is false.
4. Statement (iv): {φ}⊂A
- This statement claims that the set containing the empty set, {φ}, is a subset of A.
- For {φ} to be a subset of A, the empty set must be an element of A, which we have already established is not the case.
- Therefore, this statement is also false.
Summary of Results:
- All statements (i), (ii), (iii), and (iv) are false.
- However, the elements of A are a, b, {c,d}, and e. The set {a,b,e} is not one of these elements; rather, it is a different set.
- Therefore, this statement is false.
- For {a,b,c} to be a subset of A, all elements a, b, and c must be present in A.
- While a and b are present in A, c is not present as an individual element; instead, c is part of the nested set {c,d}.
- Therefore, this statement is false.
- The statement claims that the empty set is an element of A.
- The elements of A are a, b, {c,d}, and e, and the empty set is not listed as one of the elements.
- Therefore, this statement is false.
- For {φ} to be a subset of A, the empty set must be an element of A, which we have already established is not the case.
- Therefore, this statement is also false.
- All statements (i), (ii), (iii), and (iv) are false.
Topper's Solved these Questions
Similar Questions
Let A={a,b,{c,d}, e} . Which of the following statements are false and why? (i) a∈A (ii) a⊂A (iii) {a,b,e}⊂A
View SolutionLet A={a,b,{c,d}, e} . Which of the following statements are false and why? (i) {c,d}⊂A (ii) {c,d}∈A (iii) {{c,d}}⊂A
View SolutionLet A={{1,2,3}, {4,5}, {6,7,8}}. Determine which of the following is true or false: (i)1∈A (ii) {1,2,3}⊂A (iii) {6,7,8}∈A
View SolutionLet A={{1,2,3}, {4,5}, {6,7,8}}. Determine which of the following is true or false: (i) {{4,5}}⊂A (ii)φ∈A (iii) φ⊂A
View SolutionLet A={φ{φ},1,{1,φ},2}. Which of the following are true? (i) {{2},{1}}A (ii) {φ,{φ},{1,φ}}⊂A
View SolutionWrite down all the subsets of the following sets (i) {a} (ii) {a,b} (iii) {1,2,3} (iv) φ
View SolutionWhich of the following is/are not carrectly mathched pairs ?
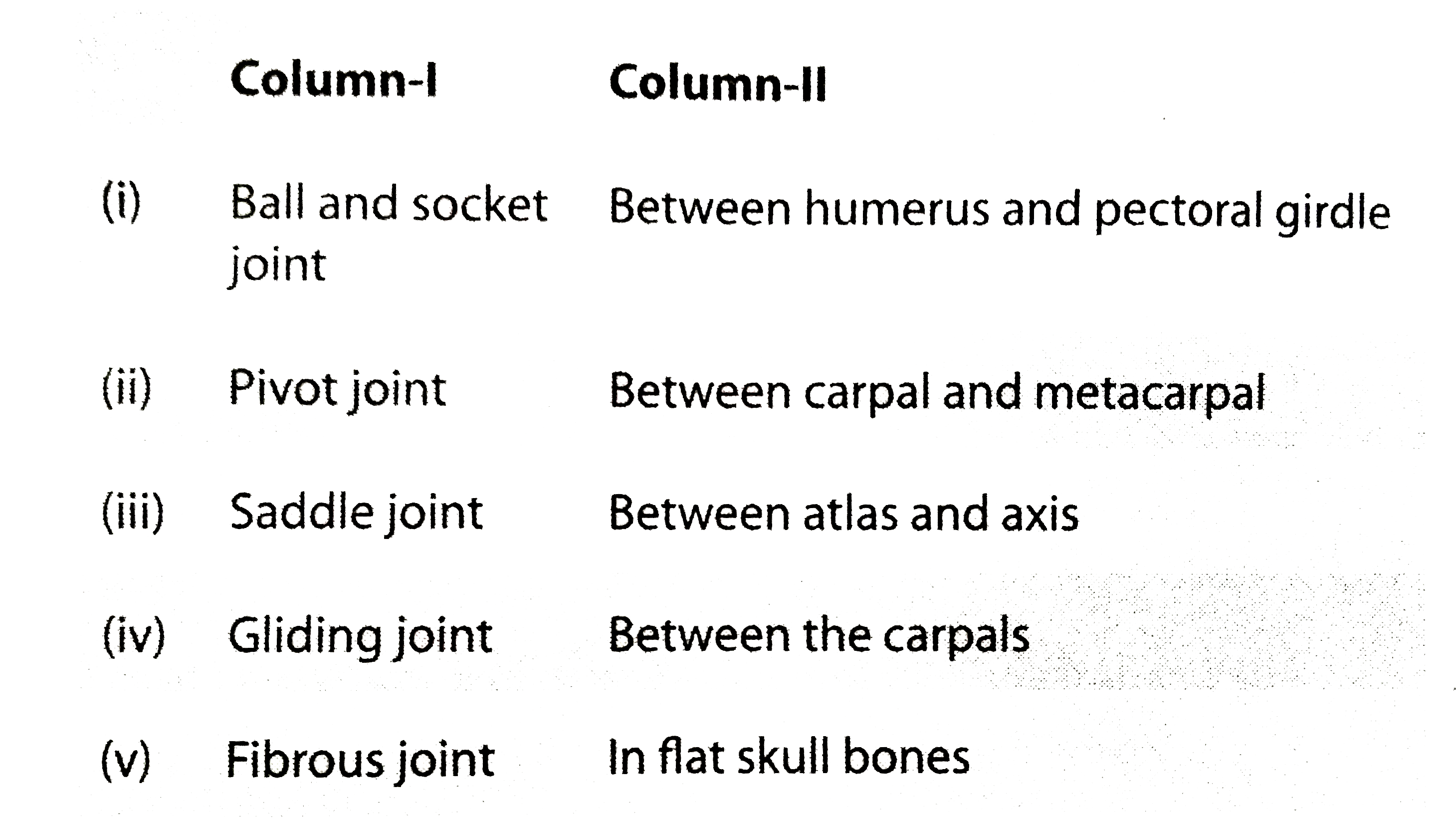
(a) (ii) and (iii)
(b) (i) and (iv)
(c) (v) only
(d) (ii) only
View SolutionIf U={a,b,c,d,e,f,g,h}, find the complements of the following sets :(i) A={a,b,c} (ii) B={d,e,f,g] (iii) C={a,c,e,g} (iv) D={f,g,h,a)
View SolutionIf U={a,b,c,d,e,f,g,h}, find the complements of the following sets :(i) A={a,b,c} (ii) B={d,e,f,g] (iii) C={a,c,e,g} (iv) D={f,g,h,a)
View SolutionLet A={φ,{φ},1,{1,φ},2}. Which of the following are true? i.φ∈A ii. 2⊂A iii. {2,{1}}⊂A
View Solution
