Question

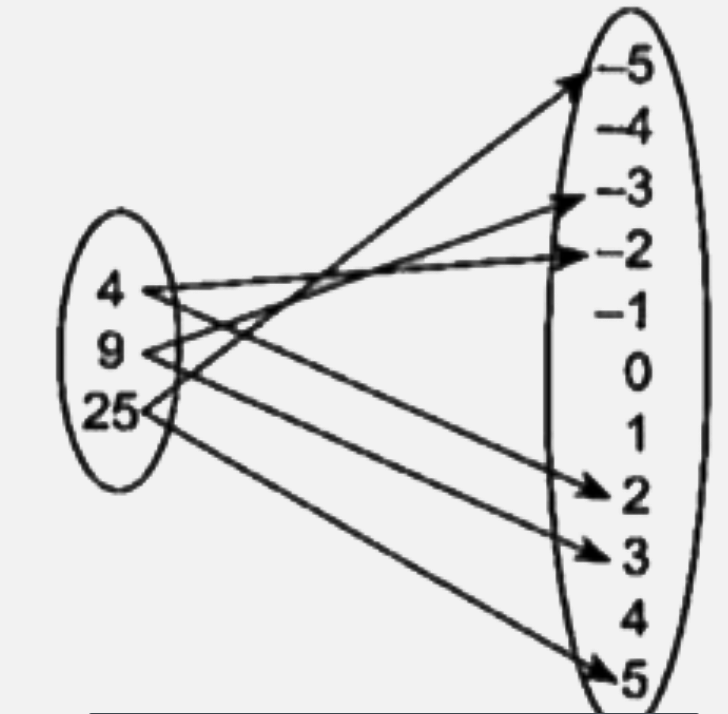
Figure 2.14 shows a relation $R$
between the sets $PandQ$
. Write this relation R in i. Roster form ii. Set builder form. What is
it's domain and range?

Explanation

To solve the problem, we will follow these steps:

Step 1: Identify the Relation R from the Figure
From the given figure (Figure 2.14), we need to identify the pairs that constitute the relation R between the sets P and Q.

Assuming the pairs are as follows based on the description:
- (9, 3)
- (9, -3)
- (4, 2)
- (4, -2)
- (25, 5)
- (25, -5)

Step 2: Write the Relation R in Roster Form
The roster form lists all the ordered pairs in the relation R.

Thus, the relation R in roster form is:
\( R = \{ (9, 3), (9, -3), (4, 2), (4, -2), (25, 5), (25, -5) \} \)

Step 3: Write the Relation R in Set Builder Form
In set builder form, we express the relation using a property that defines the elements of the relation.

From the pairs identified, we can observe that the relation seems to be defined by the square root relationship:
\( R = \{ (x, y) | y = \sqrt{x} \text{ or } y = -\sqrt{x}, x \in \{9, 4, 25\} \} \)

Step 4: Determine the Domain and Range
The domain consists of all the first elements (x-values) of the ordered pairs, and the range consists of all the second elements (y-values).

- Domain: The set of x-values is {9, 4, 25}.
- Range: The set of y-values is {3, -3, 2, -2, 5, -5}.

Final Answer
1. Roster Form:
\( R = \{ (9, 3), (9, -3), (4, 2), (4, -2), (25, 5), (25, -5) \} \)

2. Set Builder Form:
\( R = \{ (x, y) | y = \sqrt{x} \text{ or } y = -\sqrt{x}, x \in \{9, 4, 25\} \} \)

3. Domain: {9, 4, 25}

4. Range: {3, -3, 2, -2, 5, -5}