Define a function as a correspondence between two sets.
To define a function as a correspondence between two sets, we can follow these steps:
Step 1: Define the Sets
A function is a relationship between two sets. Let's denote these sets as:
- Set A (the domain)
- Set B (the range)
Step 2: Define the Correspondence
A function establishes a correspondence between the elements of Set A and Set B. This means that for every element in Set A, there is a specific element in Set B.
Step 3: Unique Output for Each Input
In a function, each input from Set A must correspond to exactly one output in Set B. This is a key characteristic that distinguishes functions from general relations, where an input can correspond to multiple outputs.
Step 4: Example of a Function
For example, consider:
- Set A = {0, 1, 2, 3}
- Set B = {p, q, r, s}
We can define a function f from Set A to Set B as:
- f(0) = p
- f(1) = q
- f(2) = r
- f(3) = s
Here, each element of Set A (the domain) corresponds to exactly one element of Set B (the range).
Step 5: Conclusion
Thus, we can conclude that a function is a special type of correspondence between two sets where each element of the first set (domain) is paired with exactly one element of the second set (range).
---
A function is a relationship between two sets. Let's denote these sets as:
- Set A (the domain)
- Set B (the range)
A function establishes a correspondence between the elements of Set A and Set B. This means that for every element in Set A, there is a specific element in Set B.
In a function, each input from Set A must correspond to exactly one output in Set B. This is a key characteristic that distinguishes functions from general relations, where an input can correspond to multiple outputs.
For example, consider:
- Set A = {0, 1, 2, 3}
- Set B = {p, q, r, s}
- f(0) = p
- f(1) = q
- f(2) = r
- f(3) = s
Thus, we can conclude that a function is a special type of correspondence between two sets where each element of the first set (domain) is paired with exactly one element of the second set (range).
Topper's Solved these Questions
Similar Questions
Define a functional group.
View SolutionDefine a function as a set of ordered pairs.
View SolutionDefine work function of a metal.
View SolutionDefine continuity of a function at a point.
View SolutionUser defined functions reside in classes
View SolutionWhich of the following is the wrong function of the corresponding part in the angiosperm plant ?
View SolutionDefine a binary operation on a set.
View Solution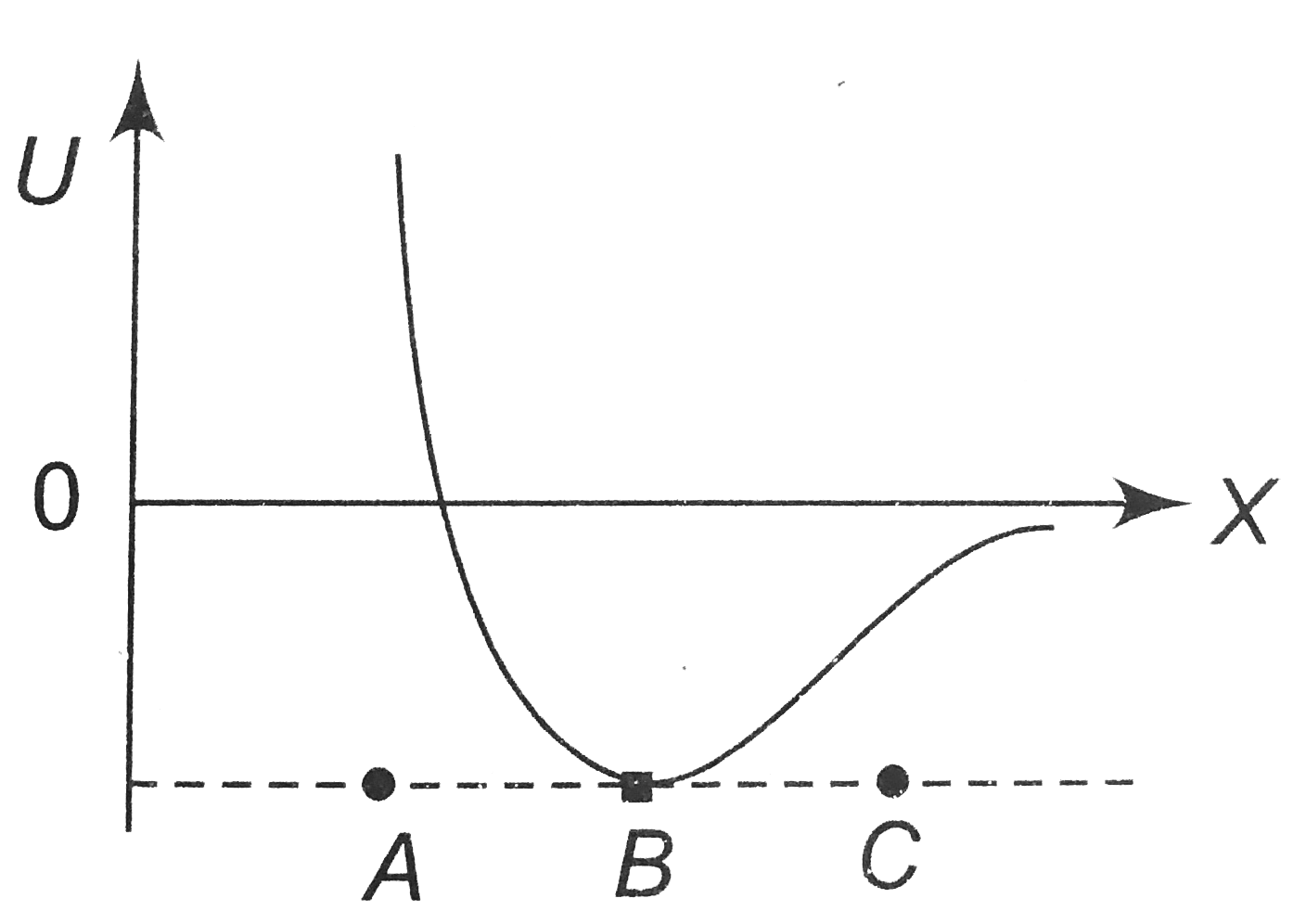
The potential energy U between two molecules as a function of the distance X between them has been shown in the figure. The two molecules are
View Solution
The potential energy U between two molecules as a function of the distance X between them has been shown in the figure. The two molecules are
View SolutionDefine the term 'mutual inductance' between the two coils.
View Solution