A horse is tied to a post by a rope. If the horse moves along a circular path always keeping the rope tight, and describes 88 metres when it traces 72∘ at the centre, find the length of the rope.
To solve the problem, we need to find the length of the rope (which we'll denote as r) based on the information provided about the arc length and the angle traced by the horse. Here's a step-by-step solution:
Step 1: Understand the relationship between arc length, radius, and angle
The relationship between the arc length s, radius r, and angle θ (in radians) is given by the formula:
s=r⋅θ
Where:
- s is the arc length (88 meters in this case),
- r is the radius (length of the rope),
- θ is the angle in radians.
Step 2: Convert the angle from degrees to radians
We are given the angle θ=72∘. To convert this to radians, we use the conversion factor π180:
θ=72⋅π180=72π180=2π5 radians
Step 3: Substitute the values into the arc length formula
Now we can substitute the known values into the arc length formula:
88=r⋅2π5
Step 4: Solve for the radius r
To find r, we rearrange the equation:
r=88⋅52π
Step 5: Simplify the expression
Now we simplify the expression:
r=4402π=220π
Step 6: Substitute π with 227 for calculation
Using π≈227:
r=220227=220⋅722=10⋅7=70 meters
Conclusion
Thus, the length of the rope is:
70 meters
The relationship between the arc length s, radius r, and angle θ (in radians) is given by the formula:
s=r⋅θ
Where:
- s is the arc length (88 meters in this case),
- r is the radius (length of the rope),
- θ is the angle in radians.
We are given the angle θ=72∘. To convert this to radians, we use the conversion factor π180:
θ=72⋅π180=72π180=2π5 radians
Now we can substitute the known values into the arc length formula:
88=r⋅2π5
To find r, we rearrange the equation:
r=88⋅52π
Now we simplify the expression:
r=4402π=220π
Using π≈227:
r=220227=220⋅722=10⋅7=70 meters
Thus, the length of the rope is:
70 meters
Topper's Solved these Questions
Similar Questions
A horse is tethered to a stake by a rope 810 cm long. If the horse moves along the circumference of a circle always keeping the rope tight, find how far it will have gone when the rope has traced out an angle of 70∘?
View SolutionA small ball of mass m and charge q is attached to the bottom end of a piece of negligible mass thread of length l, whose top end is fixed. The system formed by the thread and ball is in vertical plane and is in uniform horizontal magnetic field B, which is perpendicular to the plane of figure and points into the paper

The ball is started with a velocity v0 from lower most point of circle in a direction perpendicular both to the magnetic induction and to direction of thread. The ball moves along a circular path such that thread remains tight during the whole motion. Neglect any loss of enery.
What is the magnitude of magnetic induction B, if the minimum initial speed at which the described motion of ball (complete vertical circular motion) occurs is V0=12√17gLView SolutionStatement-I : When the direction of motion of a particle moving in a circular path is reversed the direction of radial acceleration still remains the same (at the given point).
Statement-II : Particle revolves on circular path in any direction such as clockwise or anticlockwise the direction of radius accelerationis always towards the centre of the circular path.View SolutionA small ball of mass m and charge q is attached to the bottom end of a piece of negligible mass thread of length l, whose top end is fixed. The system formed by the thread and ball is in vertical plane and is in uniform horizontal magnetic field B, which is perpendicular to the plane of figure and points into the paper

The ball is started with a velocity v0 from lower most point of circle in a direction perpendicular both to the magnetic induction and to direction of thread. The ball moves along a circular path such that thread remains tight during the whole motion. Neglect any loss of enery.
Choose CORRECT statementView SolutionA rope, under tension of 200N and fixed at both ends, oscialltes in a second harmonic standing wave pattern. The displacement of the rope is given by y=(0.10)sin(πx3)sin(12πt), where x=0 at one end of the rope, x is in metres and t is in seconds. Find the length of the rope in metres.
View SolutionOne end of a 60m long rope of mass 1.8 kg is tied to a rigid horizontal support held high above the ground. The rope hangs vertically and kept taut by a weight 'W' suspended at its lower end. A person jerks the lower end of the rope sideways in a sinusoidal manner and a transverse wave of frequency 2 Hz and amplitude 10cm passes along the rope such that there are 2 cycles of the wave in the total length of the rope. Neglecting the weight of the rope as compared to the suspended weight W and with g = 10m/s2, answer the following questions. (S=75×10−4m2)

In the questions above, weight of the rope has been neglected as compared to the suspended weight. However, if we also account for the weight of the rope. the speed of the wave at the top of the rope will beView SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.View SolutionThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
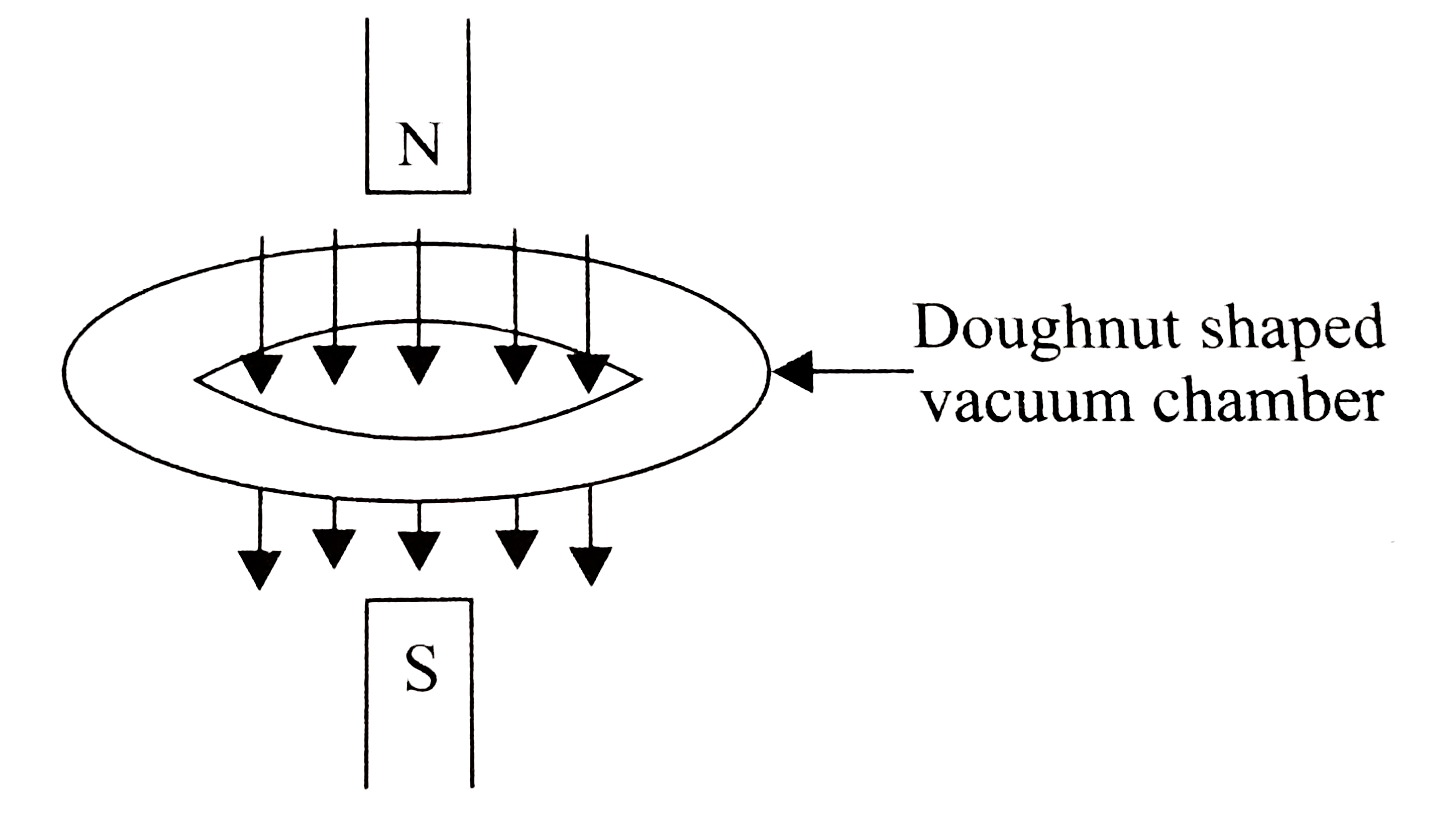
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Magnetic field which keeps the particles in circular path mustView SolutionA cat of mass m = 1 kg climbs to a rope hung over a leight frictionless pulley. The opposite end of the rope is tied to a weight of mass M = 2m lying on a smooth horizontal plane. What is the tension of the rope when the cat move upwards with in acceleration a=2m/s2 relative to the rope ?
 View Solution
View SolutionA horse runs along a circle with a speed of 20km/h . A lantern is at the centre of the circle. A fence is along the tangent to the circle at the point at which the horse starts. Find the speed with which the shadow of the horse moves along the fence at the moment when it covers 1/8 of the circle in km/h.
View Solution

