If tanθ+secθ=√3,0 <θ<π, then θ is equal to a. 5π6 b. 2π3 c. π6 d. π3
To solve the equation tanθ+secθ=√3 for 0<θ<π, we can follow these steps:
Step 1: Rewrite the equation
We start with the equation:
tanθ+secθ=√3
We can express secθ in terms of tanθ:
secθ=√3−tanθ
Step 2: Use the identity for sec2θ
Recall the Pythagorean identity:
sec2θ=1+tan2θ
Substituting secθ into this identity, we square both sides:
sec2θ=(√3−tanθ)2
Step 3: Expand the right-hand side
Expanding the right-hand side gives:
sec2θ=3−2√3tanθ+tan2θ
Step 4: Set up the equation
Now, substituting sec2θ from the identity:
1+tan2θ=3−2√3tanθ+tan2θ
Step 5: Simplify the equation
Subtract tan2θ from both sides:
1=3−2√3tanθ
Rearranging gives:
2√3tanθ=3−1
2√3tanθ=2
Step 6: Solve for tanθ
Dividing both sides by 2√3:
tanθ=22√3=1√3
Step 7: Find the angle θ
The value of tanθ=1√3 corresponds to:
θ=π6
Step 8: Check the range
Since 0<θ<π, θ=π6 is a valid solution.
Final Answer
Thus, the value of θ is:
θ=π6
We start with the equation:
tanθ+secθ=√3
We can express secθ in terms of tanθ:
secθ=√3−tanθ
Recall the Pythagorean identity:
sec2θ=1+tan2θ
Substituting secθ into this identity, we square both sides:
sec2θ=(√3−tanθ)2
Expanding the right-hand side gives:
sec2θ=3−2√3tanθ+tan2θ
Now, substituting sec2θ from the identity:
1+tan2θ=3−2√3tanθ+tan2θ
Subtract tan2θ from both sides:
1=3−2√3tanθ
Rearranging gives:
2√3tanθ=3−1
2√3tanθ=2
Dividing both sides by 2√3:
tanθ=22√3=1√3
The value of tanθ=1√3 corresponds to:
θ=π6
Since 0<θ<π, θ=π6 is a valid solution.
Thus, the value of θ is:
θ=π6
Topper's Solved these Questions
Similar Questions
If tanθ+cotθ=3, then tan4θ+cot4θ=
View SolutionThe number of distinct solutions of secθ+tanθ=√3, 0≤θ≤3π, is
View Solutionlf α and β are two different solutions lying between −π2 and π2 of the equation 2tanθ+Secθ=2 then tanα+tanβ
View SolutionIf tanθ=34 then find the value of cos2θ−sin2θ?
View SolutionIf θ is an acute angle and tanθ+cotθ=2 , find the value of tan7θ+cot7θ.
View Solution√1+sinθ1−sinθ is equal to
(a)secθ+tanθ
(b) secθ−tanθ
(c) sec 2 θ+ tan 2 θ
(d) sec 2 θ− tan 2 θ
View Solution(1+tanθ+secθ)( 1+cotθ−cosec θ )= (a) 0 (b) 2 (c) 1 (d) −1
View SolutionAn L-shaped object, made of thin rods of uniform mass density, is suspended with a string as shown in figure. If AB=BD, and the angle made by AB with downward vertical is θ, then :
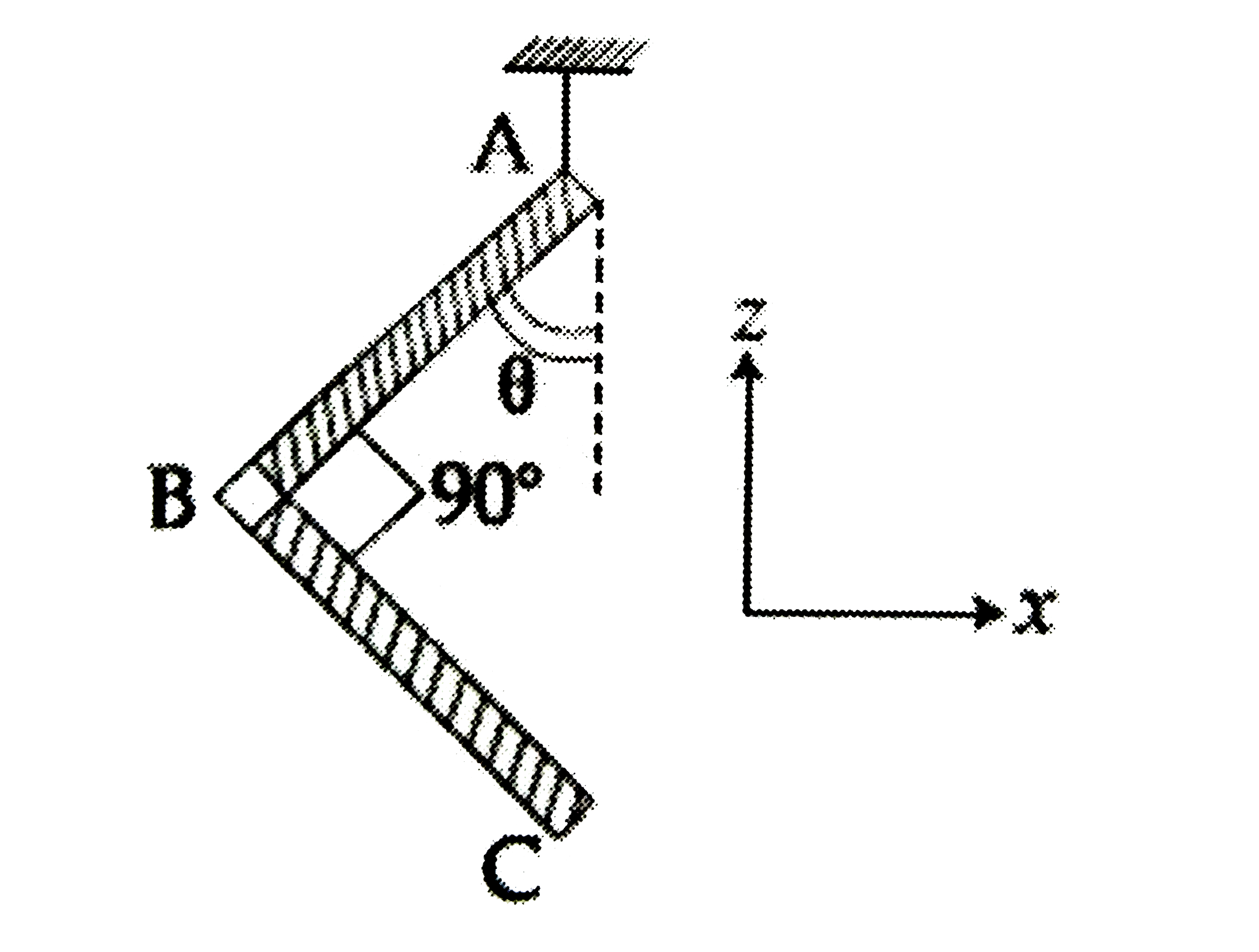 a) tanθ=1/2√3
b) tanθ=1/2
c) tanθ=2/√3
d) tanθ=1/3
a) tanθ=1/2√3
b) tanθ=1/2
c) tanθ=2/√3
d) tanθ=1/3
View SolutionIf 4sinθ+3cosθ=5 then tanθ=
View Solutioncosθ1−tanθ + sinθ1−cotθ is equals to
View Solution
