There are 10 persons named P1,P2,P3...,P10. Out of 10 persons, 5 persons are to be arranged in a line such that is each arrangement P1 must occur whereas P4 and P5 do not occur. Find the number of such possible arrangements.
To solve the problem of arranging 5 persons out of 10 such that P1 must be included while P4 and P5 must be excluded, we can follow these steps:
1. Identify the total persons and restrictions:
- We have 10 persons: P1,P2,P3,P4,P5,P6,P7,P8,P9,P10.
- We need to arrange 5 persons in a line.
- P1 must be included in the arrangement.
- P4 and P5 must not be included in the arrangement.
2. Determine the available persons:
- Since P1 must be included, we count it as one of our selected persons.
- We cannot use P4 and P5, so we exclude them from our selection.
- The remaining persons available for selection are: P2,P3,P6,P7,P8,P9,P10.
- This gives us a total of 7 persons available for selection (excluding P1, P4, and P5).
3. Calculate the number of persons to select:
- Since P1 is already included, we need to select 4 more persons from the remaining 7 persons.
- The number of ways to choose 4 persons from 7 can be calculated using the combination formula \( C(n, r) \), which is given by:
\(
C(n, r) = \frac{n!}{r!(n-r)!}
\)
- Here, \( n = 7 \) and \( r = 4 \):
\(
C(7, 4) = \frac{7!}{4! \cdot (7-4)!} = \frac{7!}{4! \cdot 3!} = \frac{7 \times 6 \times 5}{3 \times 2 \times 1} = 35
\)
4. Calculate the arrangements:
- After selecting 4 persons from the 7, we will have a total of 5 persons (including P1) to arrange.
- The number of ways to arrange 5 persons is given by \( 5! \):
\(
5! = 5 \times 4 \times 3 \times 2 \times 1 = 120
\)
5. Calculate the total arrangements:
- The total number of arrangements is the product of the number of ways to choose the persons and the number of arrangements of those persons:
\(
\text{Total arrangements} = C(7, 4) \times 5! = 35 \times 120 = 4200
\)
Final Answer:
The number of arrangements of 5 persons such that P1 is included and P4 and P5 are excluded is 4200.
- We have 10 persons: P1,P2,P3,P4,P5,P6,P7,P8,P9,P10.
- We need to arrange 5 persons in a line.
- P1 must be included in the arrangement.
- P4 and P5 must not be included in the arrangement.
- Since P1 must be included, we count it as one of our selected persons.
- We cannot use P4 and P5, so we exclude them from our selection.
- The remaining persons available for selection are: P2,P3,P6,P7,P8,P9,P10.
- This gives us a total of 7 persons available for selection (excluding P1, P4, and P5).
- Since P1 is already included, we need to select 4 more persons from the remaining 7 persons.
- The number of ways to choose 4 persons from 7 can be calculated using the combination formula \( C(n, r) \), which is given by:
\(
C(n, r) = \frac{n!}{r!(n-r)!}
\)
- Here, \( n = 7 \) and \( r = 4 \):
\(
C(7, 4) = \frac{7!}{4! \cdot (7-4)!} = \frac{7!}{4! \cdot 3!} = \frac{7 \times 6 \times 5}{3 \times 2 \times 1} = 35
\)
- After selecting 4 persons from the 7, we will have a total of 5 persons (including P1) to arrange.
- The number of ways to arrange 5 persons is given by \( 5! \):
\(
5! = 5 \times 4 \times 3 \times 2 \times 1 = 120
\)
- The total number of arrangements is the product of the number of ways to choose the persons and the number of arrangements of those persons:
\(
\text{Total arrangements} = C(7, 4) \times 5! = 35 \times 120 = 4200
\)
The number of arrangements of 5 persons such that P1 is included and P4 and P5 are excluded is 4200.
Topper's Solved these Questions
Similar Questions
10 persons are to be arranged in a circular fashion so that in no two arrangements all the persons have same neighbours. The number of ways of doing so is equal to:
View SolutionFind the magnetic field at P due to the arrangement shown
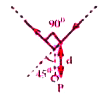
View SolutionFind the magnetic field at P due to the arrangement shown
 .
.
View SolutionIn the shown arrangement magentic field at P is :
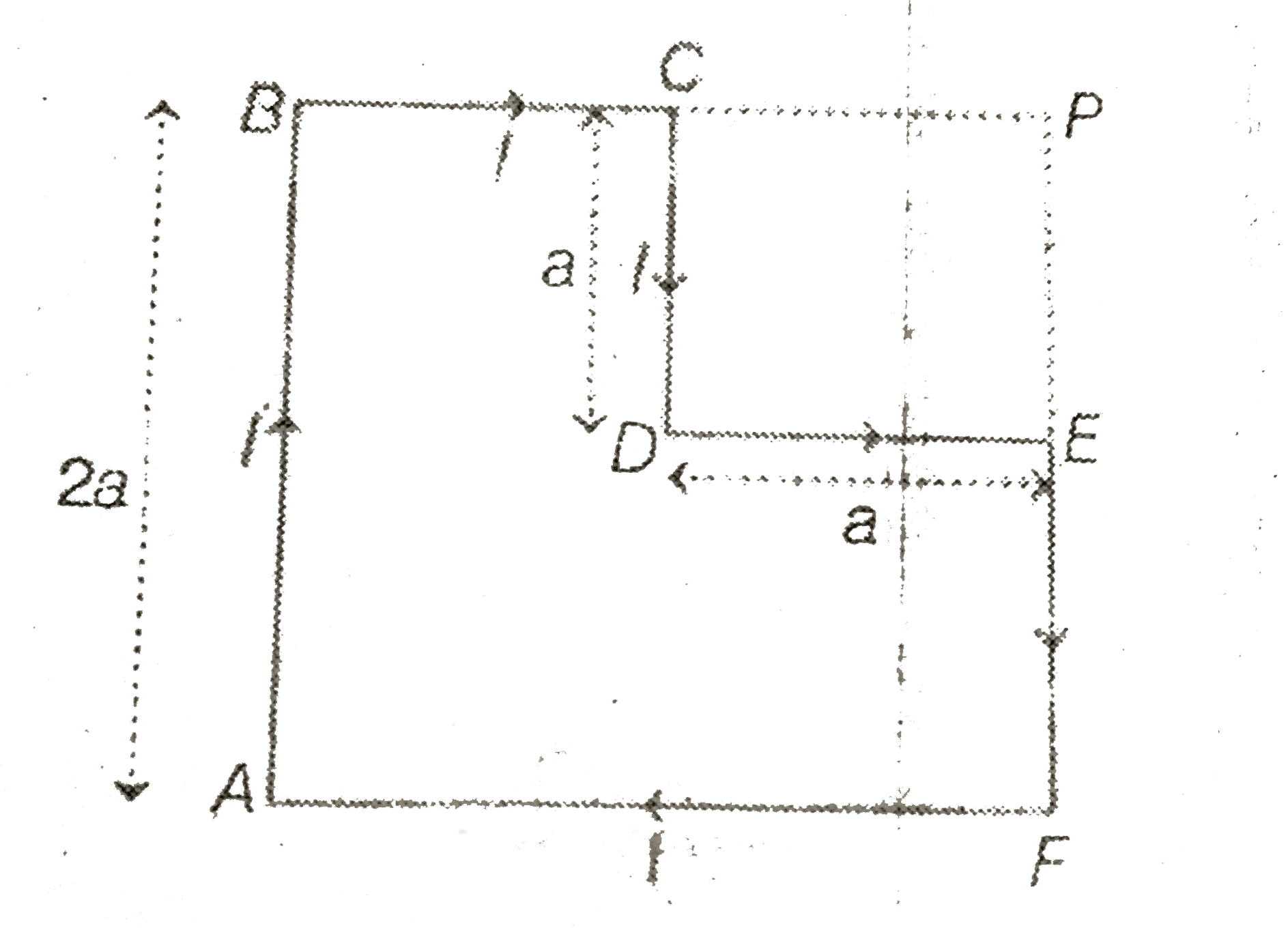
View SolutionArrange in order of increasing I.P.
View SolutionIf A and B are independent events such that P(A)=p, P(B)=2p and P (Exactly one of A and B occurs )=59 , find the value of p.
View SolutionIf A and B are events of a random experiment such that P(A∩B)=45P(A'∩B')=710 and P(B)=25, then find the value of P(A).
View Solution4d, 5p, 5f and 6p orbitals are arranged in the order of decreasing energy. The correct option is :
View SolutionA person sells an article for Rs 550, gaining 110 of its C.P. Find gain percent.
View SolutionIF P1,P2,P3,P4 are points in a plane or space and O is the origin of vectors, show that P4 coincides with O⇔(→OP)1+→P1P2+→P2P3+→P3P4=→0.
View Solution