If a is the G.M. of 2 and14, find a.
To find the geometric mean A of the numbers 2 and 14, we can follow these steps:
1. Identify the formula for the geometric mean:
The geometric mean A of two numbers x and y is given by the formula:
A=√xy
2. Substitute the values of x and y:
Here, x=2 and y=14. Substituting these values into the formula gives:
A=√2⋅14
3. Calculate the product inside the square root:
Now, calculate the product:
2⋅14=24=12
4. Take the square root:
Now, we find the square root of 12:
A=√12=1√2
5. Rationalize the denominator (optional):
If needed, we can rationalize the denominator:
A=1√2⋅√2√2=√22
Thus, the geometric mean A is:
A=1√2orA=√22
The geometric mean A of two numbers x and y is given by the formula:
A=√xy
Here, x=2 and y=14. Substituting these values into the formula gives:
A=√2⋅14
Now, calculate the product:
2⋅14=24=12
Now, we find the square root of 12:
A=√12=1√2
If needed, we can rationalize the denominator:
A=1√2⋅√2√2=√22
A=1√2orA=√22
Topper's Solved these Questions
Similar Questions
If m is the A.M. of two distinct real numbers l and n(l,n>1) and G1, G2 and G3 are three geometric means between l and n, then G14+2G24+G34 equals, (1) 4l2 mn (2) 4lm^2 mn (3) 4lmn2 (4) 4l2m2n2
View SolutionFind the area bounded by the x-axis, part of the curve y=(1+8x2) , and the ordinates at x=2andx=4. If the ordinate at x=a divides the area into two equal parts, then find a.
View SolutionIf the G.M. of a and b is an+bnan−1+bn−1 then find the value of n.
View SolutionIf the A.M. between two positive numbers exceeds their G.M. by 2 and the ratio of the numbers
be 1:4 find the numbers .
View SolutionState whether each of the following statements are true or false. If the statement is false re-write the given statement correctly: (i) If p={m,n}and Q={n,m}, then P×Q={(m,n), (n,m)} (ii) If A and B are non empty sets then A×B is a non empty set of ordered pairs (x,y) such that x∈B and y∈A. (iii)If A={1,2}, B={3,4}, then A×(B∩φ)=φ.
View SolutionIn Fig.70. if l||m||n and ∠1=60∘, find ∠2.
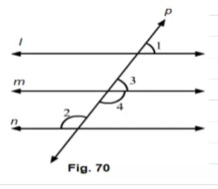
View SolutionIn Fig.72, If lm, np and ∠1=850, find ∠2.
View SolutionIf ∣∣→a×→b∣∣2=(→a.→b)2=144 and |→a|=4, find →b.
View SolutionIf →a and →b are two vectors such that ∣∣→a×→b∣∣=3 and →a.→b=1, find the angle between →a and →b .
View SolutionFind the rational number between −23and14.
View Solution
