The Fahrenheit temperature F and absolute temperature K satisfy a linear equation. Given that K = 273 when F = 32 and that K = 373 whenF = 212 . Express K in terms of F and find the value of F, when K = 0 .
To solve the problem, we need to express the absolute temperature K in terms of the Fahrenheit temperature F using the given data points, and then find the value of F when K=0.
Step 1: Identify the Points
We are given two points based on the temperature conversions:
- Point A: (F1,K1)=(32,273)
- Point B: (F2,K2)=(212,373)
Step 2: Calculate the Slope (m)
The slope m of the line connecting these two points can be calculated using the formula:
m=K2−K1F2−F1
Substituting the values:
m=373−273212−32=100180=59
Step 3: Write the Equation of the Line
Using the point-slope form of the equation of a line:
K−K1=m(F−F1)
Substituting K1=273, F1=32, and m=59:
K−273=59(F−32)
Step 4: Rearranging the Equation
Now, we can rearrange this equation to express K in terms of F:
K=59(F−32)+273
Distributing 59:
K=59F−5×329+273
Calculating 5×329:
5×329=1609
Thus, the equation becomes:
K=59F+273−1609
Converting 273 into a fraction with a denominator of 9:
273=273×99=24579
Now, combine the terms:
K=59F+2457−1609=59F+22979
Step 5: Find the Value of F when K = 0
Now, we need to find F when K=0:
0=59F+22979
Multiplying through by 9 to eliminate the fraction:
0=5F+2297
Solving for F:
5F=−2297
F=−22975=−459.4
Final Answer
The value of F when K=0 is:
F=−459.4
We are given two points based on the temperature conversions:
- Point A: (F1,K1)=(32,273)
- Point B: (F2,K2)=(212,373)
The slope m of the line connecting these two points can be calculated using the formula:
m=K2−K1F2−F1
Substituting the values:
m=373−273212−32=100180=59
Using the point-slope form of the equation of a line:
K−K1=m(F−F1)
Substituting K1=273, F1=32, and m=59:
K−273=59(F−32)
Now, we can rearrange this equation to express K in terms of F:
K=59(F−32)+273
Distributing 59:
K=59F−5×329+273
Calculating 5×329:
5×329=1609
Thus, the equation becomes:
K=59F+273−1609
Converting 273 into a fraction with a denominator of 9:
273=273×99=24579
Now, combine the terms:
K=59F+2457−1609=59F+22979
Now, we need to find F when K=0:
0=59F+22979
Multiplying through by 9 to eliminate the fraction:
0=5F+2297
Solving for F:
5F=−2297
F=−22975=−459.4
The value of F when K=0 is:
F=−459.4
Topper's Solved these Questions
Similar Questions
The fahrenheit 'F' and Kelvin 'K' temperatures show a linear relation. If at F=32, K=273 and at F=212, K=373, then find K in terms of F. Also find the value of F when K=0.
View SolutionA Kelvin scale reads temperature to be 318 K. What is the temperature in ∘C and in ∘F?
View SolutionWater freezes at 32∘F What will be the temperature in degree Celsius and K
View SolutionThe average temperature in Udhagamandalam (Ooty) is 74∘F What is the temperature in the Celsius scale? What will be the temperature in K?
View SolutionAt a given temperature, When an acid is added to water then the value of Kw
View SolutionFind the derivative of f(x)=k at x=0 and x=2.
View SolutionThe value of kf depends on nature of
View Solution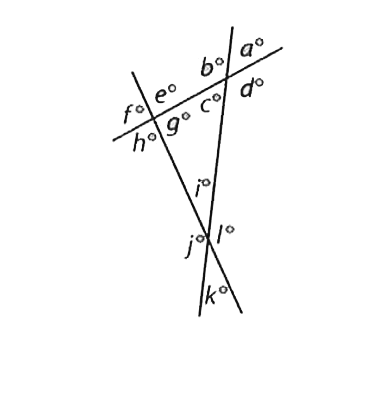
If f+k=150, find b.
View SolutionFind the derivative of f(x)=k a t x=0 and x=5.
View Solution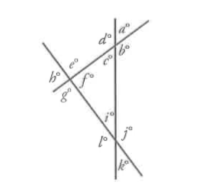
If f+k=150, find b.
View Solution
