Question

The line ${\displaystyle 2x+3y=12}$
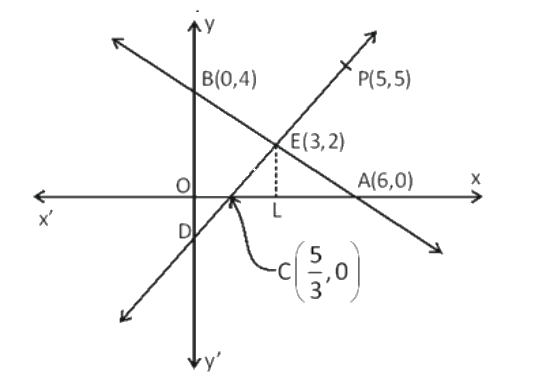
meets the x-axis at A and y-axis at B. The line through (5,5)
perpendicular to AB meets the x-axis and the line AB at C and E respectively.
If O is the origin of coordinates, find the area of figure OCEB.

Explanation

To solve the problem step by step, we will follow these instructions:

Step 1: Find the coordinates of points A and B
The line given is \(2x + 3y = 12\).

Finding point A (where the line meets the x-axis):
To find the x-intercept (point A), set \(y = 0\):
\( 2x + 3(0) = 12 \implies 2x = 12 \implies x = 6 \)
Thus, the coordinates of point A are \(A(6, 0)\).

Finding point B (where the line meets the y-axis):
To find the y-intercept (point B), set \(x = 0\):
\( 2(0) + 3y = 12 \implies 3y = 12 \implies y = 4 \)
Thus, the coordinates of point B are \(B(0, 4)\).

Step 2: Determine the slope of line AB
The slope \(m\) of line AB can be calculated using the coordinates of points A and B:
\( m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{4 - 0}{0 - 6} = \frac{4}{-6} = -\frac{2}{3} \)

Step 3: Find the slope of the line perpendicular to AB
The slope of the line perpendicular to AB is the negative reciprocal of the slope of AB:
\( m_{\perpendicular} = \frac{3}{2} \)

Step 4: Write the equation of the line through point (5, 5) with the perpendicular slope
Using point-slope form \(y - y_1 = m(x - x_1)\):
\( y - 5 = \frac{3}{2}(x - 5) \)
Expanding this:
\( y - 5 = \frac{3}{2}x - \frac{15}{2} \)
Rearranging gives:
\( 3x - 2y - 5 = 0 \)

Step 5: Find the intersection point E of the two lines
To find point E, we need to solve the equations of the two lines:
1. \(2x + 3y = 12\)
2. \(3x - 2y - 5 = 0\)

From the second equation, express \(y\):
\( 2y = 3x - 5 \implies y = \frac{3}{2}x - \frac{5}{2} \)
Substituting this into the first equation:
\( 2x + 3\left(\frac{3}{2}x - \frac{5}{2}\right) = 12 \)
Simplifying:
\( 2x + \frac{9}{2}x - \frac{15}{2} = 12 \)
Multiplying through by 2 to eliminate the fraction:
\( 4x + 9x - 15 = 24 \implies 13x = 39 \implies x = 3 \)
Substituting \(x = 3\) back to find \(y\):
\( y = \frac{3}{2}(3) - \frac{5}{2} = \frac{9}{2} - \frac{5}{2} = 2 \)
Thus, the coordinates of point E are \(E(3, 2)\).

Step 6: Find the coordinates of point C (where the line meets the x-axis)
To find point C, set \(y = 0\) in the equation of the line \(3x - 2y - 5 = 0\):
\( 3x - 2(0) - 5 = 0 \implies 3x = 5 \implies x = \frac{5}{3} \)
Thus, the coordinates of point C are \(C\left(\frac{5}{3}, 0\right)\).

Step 7: Calculate the area of quadrilateral OCEB
The area of quadrilateral OCEB can be calculated as the sum of the areas of triangles OBE and OCE.

Area of triangle OBE:
Base \(OB = 4\) (from \(O(0,0)\) to \(B(0,4)\)) and height from E to OB (horizontal distance from E to y-axis):
\( \text{Height} = 3 \text{ (x-coordinate of E)} \)
Area of triangle OBE:
\( \text{Area}_{OBE} = \frac{1}{2} \times \text{Base} \times \text{Height} = \frac{1}{2} \times 4 \times 3 = 6 \)

Area of triangle OCE:
Base \(OC = \frac{5}{3}\) and height from E to OC (vertical distance from E to x-axis):
\( \text{Height} = 2 \text{ (y-coordinate of E)} \)
Area of triangle OCE:
\( \text{Area}_{OCE} = \frac{1}{2} \times \text{Base} \times \text{Height} = \frac{1}{2} \times \frac{5}{3} \times 2 = \frac{5}{3} \)

Step 8: Total area of quadrilateral OCEB
\( \text{Total Area} = \text{Area}_{OBE} + \text{Area}_{OCE} = 6 + \frac{5}{3} = \frac{18}{3} + \frac{5}{3} = \frac{23}{3} \)

Thus, the area of the figure OCEB is \(\frac{23}{3}\) square units.