Find limx→0f(x)and(lim)x→1f(x),wheref(x)=[2x+3,x≤03(x+1),x>0
To solve the problem, we need to find the limits of the function f(x) as x approaches 0 and 1. The function is defined piecewise as follows:
f(x)={2x+3if x≤03(x+1)if x>0
Step 1: Find limx→0f(x)
To find the limit as x approaches 0, we need to evaluate both the left-hand limit and the right-hand limit.
Left-hand limit as x→0:
Since we are approaching from the left (where x≤0), we use the first part of the piecewise function:
limx→0−f(x)=limx→0(2x+3)
Substituting x=0:
=2(0)+3=3
Right-hand limit as x→0:
Now, we approach from the right (where x>0), so we use the second part of the piecewise function:
limx→0+f(x)=limx→03(x+1)
Substituting x=0:
=3(0+1)=3
Since both the left-hand limit and right-hand limit are equal, we conclude:
limx→0f(x)=3
Step 2: Find limx→1f(x)
Now we need to find the limit as x approaches 1. Since 1 is greater than 0, we use the second part of the piecewise function:
limx→1f(x)=limx→13(x+1)
Substituting x=1:
=3(1+1)=3×2=6
Final Results
Thus, we have:
limx→0f(x)=3
limx→1f(x)=6
Since we are approaching from the left (where x≤0), we use the first part of the piecewise function:
Now, we approach from the right (where x>0), so we use the second part of the piecewise function:
Thus, we have:
Topper's Solved these Questions
Similar Questions
Find (lim)x→1f(x),wheref(x)=[x2−1,x≤1−x2−1,x>1
View SolutionEvaluate (lim)x→0f(x), where f(x)={|x|x, x≠0,0, x=0
View SolutionEvaluate limx→0f(x), where
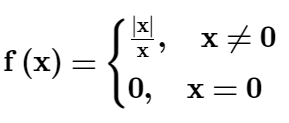
View SolutionFind limx→1f(x), where f(x)={x+1x≠10x=1}
View SolutionFind limx→0f(x), where f(x)=⎧⎪⎨⎪⎩x−1x<00x=0x=1x>0
View Solutionlimx→0etanx−extanx−x=
View SolutionFind limx→0f(x) where
f(x)={x|x|x≠00x=0
View SolutionEvaluate : limx→0(1−x)n−1x
View SolutionLet f(x) is a function continuous for all x∈R except at x = 0 such that f'(x)<0,∀x∈(−∞,0)andf'(x)>0,∀x∈(0,∞). If limx→0+f(x)=3,limx→0−f(x)=4andf(0)=5, then the image of the point (0, 1) about the line, y.limx→0f(cos3x−cos2x)=x.limx→0f(sin2x−sin3x), is
View Solutionlimx→0(1−ex)sinxx2+x3 is equal to
View Solution
