Write a value of
To solve the integral ∫sinx+cosx√1+sin2xdx, we can follow these steps:
1. Rewrite the integral:
∫sinx+cosx√1+sin2xdx
2. Use trigonometric identities:
Recall that:
- sin2x=2sinxcosx
- sin2x+cos2x=1
Therefore, we can rewrite 1+sin2x as:
1+sin2x=1+2sinxcosx=sin2x+cos2x+2sinxcosx=(sinx+cosx)2
3. Substitute this back into the integral:
Now, we can substitute this into the integral:
√1+sin2x=√(sinx+cosx)2=|sinx+cosx|
Assuming sinx+cosx≥0 in the interval we are integrating over, we can simplify this to:
√1+sin2x=sinx+cosx
4. Simplify the integral:
Now substituting this back into the integral gives us:
∫sinx+cosxsinx+cosxdx=∫1dx
5. Integrate:
The integral of 1 with respect to x is:
x+C
Final Answer:
Thus, the value of the integral is:
∫sinx+cosx√1+sin2xdx=x+C
∫sinx+cosx√1+sin2xdx
Recall that:
- sin2x=2sinxcosx
- sin2x+cos2x=1
1+sin2x=1+2sinxcosx=sin2x+cos2x+2sinxcosx=(sinx+cosx)2
Now, we can substitute this into the integral:
√1+sin2x=√(sinx+cosx)2=|sinx+cosx|
Assuming sinx+cosx≥0 in the interval we are integrating over, we can simplify this to:
√1+sin2x=sinx+cosx
Now substituting this back into the integral gives us:
∫sinx+cosxsinx+cosxdx=∫1dx
The integral of 1 with respect to x is:
x+C
Thus, the value of the integral is:
∫sinx+cosx√1+sin2xdx=x+C
Topper's Solved these Questions
Similar Questions
∫(sinx+cosx√sin2xdx
View SolutionEvaluate: ∫sinx+cosx√1−sin2x dx
View SolutionEvaluate: ∫sinx+cosx√1−sin2x dx
View SolutionEvaluate: ∫sinx+cosx√1−sin2x dx
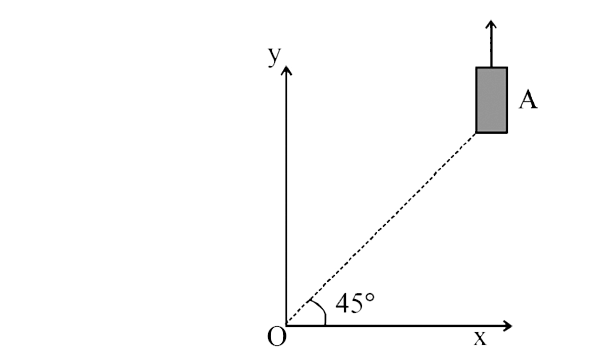
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
View SolutionEvaluate: ∫sinx−cosx√sin2xdx
View SolutionThe value of ∫sinx+cosx√1−sin2x dx is equal to
(a)√sin2x+C
(b) √cos2x+C
(c) ±(sinx−cosx)+C
(d) ±log(sinx−cosx)+C
View SolutionEvaluate ∫(sinx+cosx)dx√3+sin2x.
View SolutionThe value of ∫sinx−cosx√sin2xdx is equal to
View SolutionThe value of ∫sinx+cosx3+sin2xdx , is
View Solution
