The equation of electromotive forces for an electric circuit containing resistance and self inductance is E=R i+Ldidt, where E is the electromotive force given to the circuit, R, the resistance and L, the coefficient of induction. Find the current i at time t when (i) E=0 (ii) E=a ,non-zero constant.
To solve the given differential equation for the current i in an electric circuit with resistance R and self-inductance L, we start with the equation:
E=Ri+Ldidt
We will analyze two cases: (i) when E=0 and (ii) when E=a (a non-zero constant).
Case (i): E=0
1. Substituting E=0:
0=Ri+Ldidt
2. Rearranging the equation:
Ldidt=−Ri
3. Separating variables:
dii=−RLdt
4. Integrating both sides:
∫dii=−RL∫dt
This gives:
ln|i|=−RLt+C
5. Exponentiating both sides:
|i|=eCe−RLt
Let eC=K, then:
i=Ke−RLt
6. Determining the constant K:
If we assume that at t=0, i=0, then:
0=Ke0⟹K=0
Thus, the solution is:
i(t)=0
Case (ii): E=a (a non-zero constant)
1. Substituting E=a:
a=Ri+Ldidt
2. Rearranging the equation:
Ldidt=a−Ri
3. Separating variables:
dia−Ri=1Ldt
4. Integrating both sides:
∫dia−Ri=1L∫dt
The left side integrates to:
−1Rln|a−Ri|=tL+C
5. Exponentiating both sides:
|a−Ri|=e−R(tL+C)=Ke−RLt
where K=e−RC.
6. Solving for i:
a−Ri=Ke−RLt
Rearranging gives:
Ri=a−Ke−RLt
Therefore:
i=aR−KRe−RLt
7. Determining the constant K:
Assuming at t=0, i(0)=0:
0=aR−KR⟹K=a
Thus, the final solution is:
i(t)=aR−aRe−RLt=aR(1−e−RLt)
Summary of Solutions
- For E=0:
i(t)=0
- For E=a:
i(t)=aR(1−e−RLt)
0=Ri+Ldidt
Ldidt=−Ri
dii=−RLdt
∫dii=−RL∫dt
This gives:
ln|i|=−RLt+C
|i|=eCe−RLt
Let eC=K, then:
i=Ke−RLt
If we assume that at t=0, i=0, then:
0=Ke0⟹K=0
Thus, the solution is:
i(t)=0
a=Ri+Ldidt
Ldidt=a−Ri
dia−Ri=1Ldt
∫dia−Ri=1L∫dt
The left side integrates to:
−1Rln|a−Ri|=tL+C
|a−Ri|=e−R(tL+C)=Ke−RLt
where K=e−RC.
a−Ri=Ke−RLt
Rearranging gives:
Ri=a−Ke−RLt
Therefore:
i=aR−KRe−RLt
Assuming at t=0, i(0)=0:
0=aR−KR⟹K=a
Thus, the final solution is:
i(t)=aR−aRe−RLt=aR(1−e−RLt)
i(t)=0
i(t)=aR(1−e−RLt)
Topper's Solved these Questions
Similar Questions
A circuit contains resistance R and an inductance L in series. An alternating voltage V=V0sinωt is applied across it. The currents in R and L respectively will be
 .
.
View SolutionA circuit contains resistance R and an inductance L in series. An alternating voltage V=V0sinωt is applied across it. The currents in R and L respectively will be
 .
.
View SolutionWhen a battery is connected across a series combination of self inductance L and resistance R , the variation in the current i with time t is best represented by
View SolutionWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0. Then,
View SolutionIn Fig, the mutual inductance of a coil and a very long straight wire is M, coil has resistance R and self-inductance L. The current in the wire varies according to the law I=at, where a is a constant and t is the time, the time dependence of current in the coil is
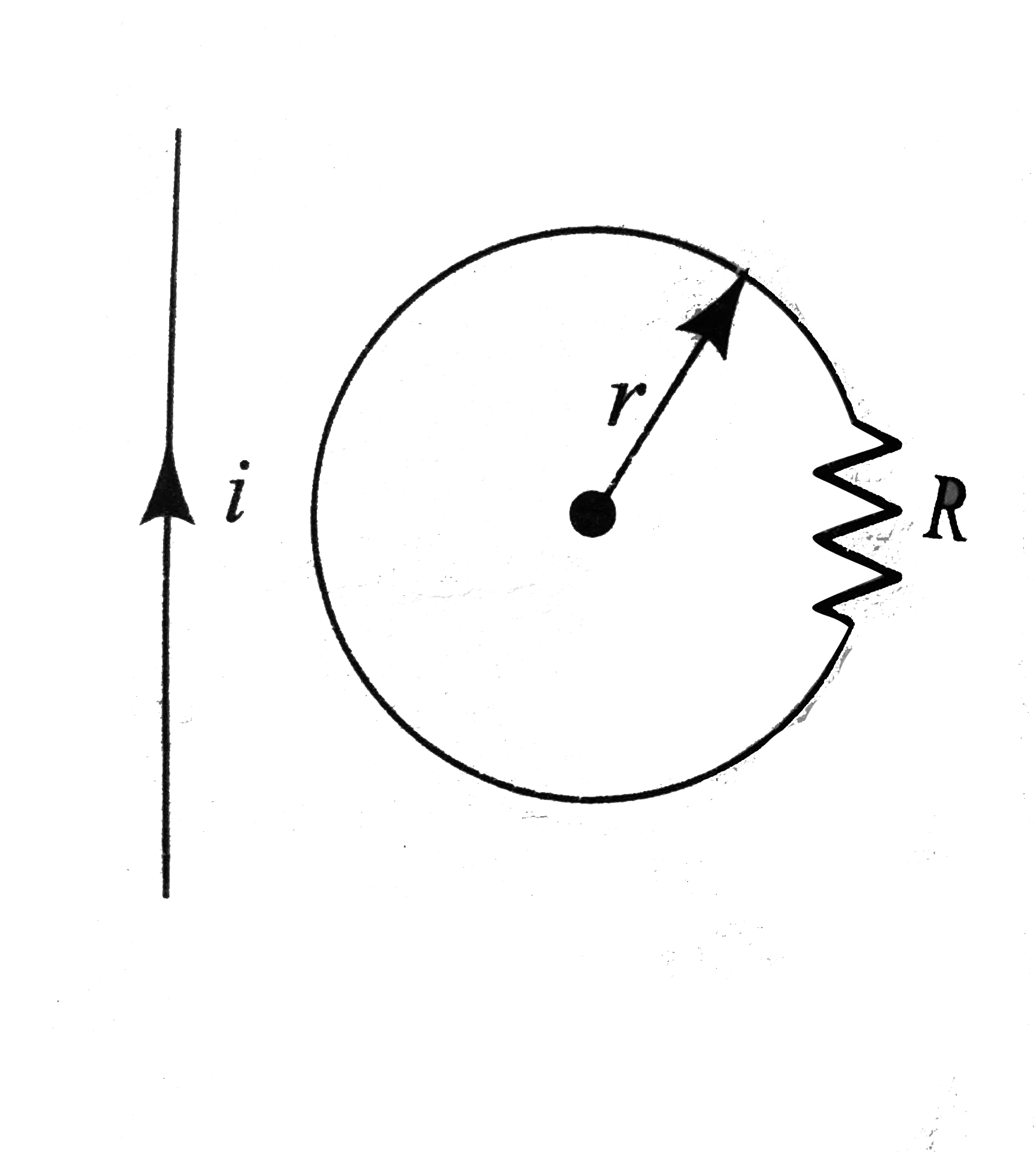
View SolutionAn alternating emf of 200V, 50Hz is applied to an L-R circuit, having a resistances R of 10Ω and an inductance L of 0.05H connected in series. Calculate:
Current flowing in the circuit
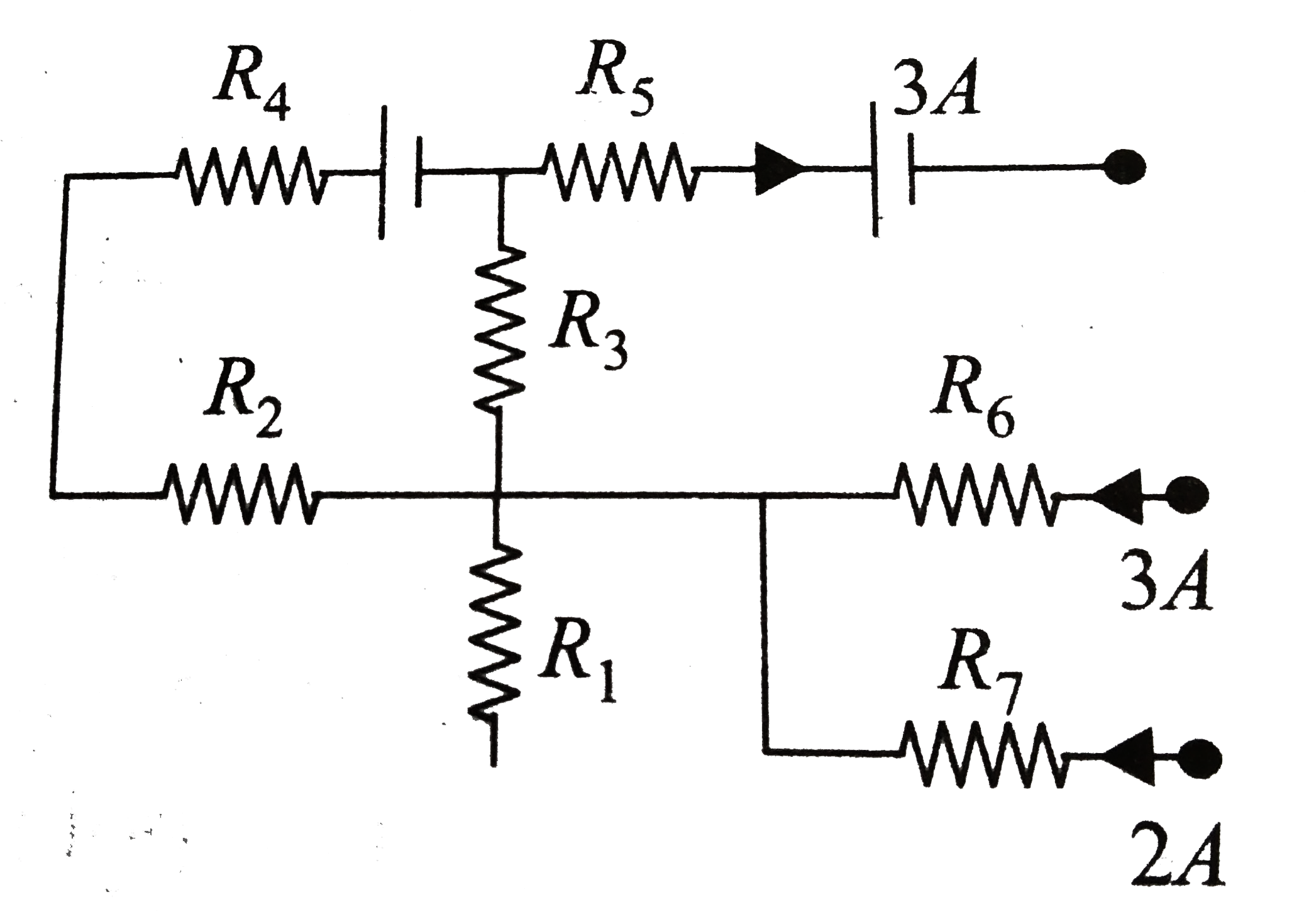
View SolutionIn the given circuit, if I1andI2 be the current in resistances R1andR2, respectively, then
 .
.
View SolutionIn an electric circuit applied ac emf is e=20sin300t volt and the current is i=4sin300t ampere. The reactance of the circuit is-
View SolutionA closed circuit consits of a source of constant and E and a choke coil of inductance L connected in series. The active resistance of the whole circuit is equal to R. At the moment t=0 the choke coil inductance was decreased abrupty η times. FInd the current in the circuit as a function of time t.
View SolutionThe current in a discharging LR circuit is given by I=i0e−tτ where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View Solution
