Writhe the component of →b along →a.
To find the component of vector b along vector a, we can follow these steps:
Step 1: Understand the Concept
The component of vector b along vector a can be found using the formula:
Component of →b along →a=→a⋅→b|→a|^a
where ^a is the unit vector in the direction of a.
Step 2: Draw the Diagram
Draw a diagram with vectors a and b originating from the same point. Label the angle between them as θ. The point where the perpendicular from b meets a can be labeled as point M.
Step 3: Use the Cosine of the Angle
In triangle OMB (where O is the origin, M is the foot of the perpendicular from b to a, and B is the tip of vector b), we can use the cosine definition:
cos(θ)=OMOB
This implies:
OM=OB⋅cos(θ)
Step 4: Express OM in Terms of Vectors
The vector OM can be expressed as:
→OM=|→b|cos(θ)^a
where |→b| is the magnitude of vector b and ^a is the unit vector in the direction of a.
Step 5: Relate Cosine to Dot Product
We know that:
cos(θ)=→a⋅→b|→a||→b|
Substituting this into our expression for OM gives:
OM=|→b|⋅→a⋅→b|→a||→b|^a
Step 6: Simplify the Expression
The magnitude of OM can be simplified:
OM=→a⋅→b|→a|^a
Step 7: Final Result
Thus, the component of vector b along vector a is:
Component of →b along →a=→a⋅→b|→a|^a
The component of vector b along vector a can be found using the formula:
Component of →b along →a=→a⋅→b|→a|^a
where ^a is the unit vector in the direction of a.
Draw a diagram with vectors a and b originating from the same point. Label the angle between them as θ. The point where the perpendicular from b meets a can be labeled as point M.
In triangle OMB (where O is the origin, M is the foot of the perpendicular from b to a, and B is the tip of vector b), we can use the cosine definition:
cos(θ)=OMOB
This implies:
OM=OB⋅cos(θ)
The vector OM can be expressed as:
→OM=|→b|cos(θ)^a
where |→b| is the magnitude of vector b and ^a is the unit vector in the direction of a.
We know that:
cos(θ)=→a⋅→b|→a||→b|
Substituting this into our expression for OM gives:
OM=|→b|⋅→a⋅→b|→a||→b|^a
The magnitude of OM can be simplified:
OM=→a⋅→b|→a|^a
Thus, the component of vector b along vector a is:
Component of →b along →a=→a⋅→b|→a|^a
Topper's Solved these Questions
Similar Questions
If →A=2ˆi+ˆj and →B=ˆi−ˆj, sketch vector graphically and find the component of →A along →B and perpendicular to →B
View SolutionIf →a and →b are two vectors such that →a.→b=6, |→a|=3 and ∣∣→b∣∣=4. Write the projection of →a on →b.
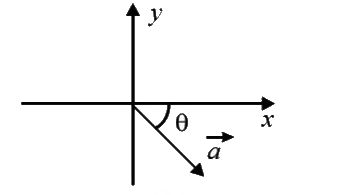
View SolutionWhat is the component of the vector →a along the x-axis in the situation shown in figure ? |→a|=5 units.
View SolutionIf →A=2ˆi+ˆj+ˆk and →B=10ˆi+5ˆj+5ˆk, if the magnitude of component of (→B−→A) along →A is 4√x. Then x will be .
View SolutionIf →aand →bare two collinear vectors, then which of the following are incorrect:(A) →b=λ→a,for some scalar lambda (B) →a=±→b (C) the respective components of →aand →bare proportional(D) both the vectors →a and →bhave same direction, but different magnitudes.
View SolutionIf |→a|=2, ∣∣→b∣∣=3 and →a.→b=3 find the projection of →b on →a.
View SolutionIf →a and →b are unit vectors then write the value of ∣∣→a×→b∣∣2+(→a.→b)2.
View SolutionIf →a and →b are unit vectors then write the value of ∣∣→a×→b∣∣2+(→a.→b)2.
View SolutionIf →a=ˆi+ˆj+ˆk,→b=ˆi−ˆj+ˆk,→c=ˆi+2ˆj−ˆk, then find the vaue of ∣∣∣→a.→a→a.→b→a.→c→b.→a→b.→a→b.→a.→c.→a.→c.→a.→c.→a∣∣∣ .
View SolutionShow that the projection vector →aand→b(≠→0)(componen→f→aaong→b)is⎛⎜⎝→a.→b∣∣→b∣∣2⎞⎟⎠→b.
View Solution
