Find a vector of magnitude 26 units normal to the plane 12x−3y+4z=1.
To find a vector of magnitude 26 units normal to the plane given by the equation 12x−3y+4z=1, we can follow these steps:
Step 1: Identify the normal vector from the plane equation
The general form of a plane equation is given by Ax+By+Cz=D. Here, the coefficients A, B, and C represent the components of the normal vector to the plane.
From the equation 12x−3y+4z=1, we can identify:
- A=12
- B=−3
- C=4
Thus, the normal vector n is:
n=12i−3j+4k
Step 2: Calculate the magnitude of the normal vector
The magnitude of a vector n=ai+bj+ck is given by:
|n|=√a2+b2+c2
For our normal vector:
|n|=√122+(−3)2+42=√144+9+16=√169=13
Step 3: Find the unit normal vector
The unit normal vector nunit can be found by dividing the normal vector by its magnitude:
nunit=n|n|=12i−3j+4k13
Step 4: Scale the unit normal vector to have a magnitude of 26
To find a vector of magnitude 26, we multiply the unit normal vector by 26:
d=26⋅nunit=26⋅(12i−3j+4k13)
Calculating this gives:
d=2613(12i−3j+4k)=2(12i−3j+4k)=24i−6j+8k
Final Answer
The vector of magnitude 26 units normal to the plane 12x−3y+4z=1 is:
d=24i−6j+8k
---
The general form of a plane equation is given by Ax+By+Cz=D. Here, the coefficients A, B, and C represent the components of the normal vector to the plane.
- A=12
- B=−3
- C=4
n=12i−3j+4k
The magnitude of a vector n=ai+bj+ck is given by:
|n|=√a2+b2+c2
|n|=√122+(−3)2+42=√144+9+16=√169=13
The unit normal vector nunit can be found by dividing the normal vector by its magnitude:
nunit=n|n|=12i−3j+4k13
To find a vector of magnitude 26, we multiply the unit normal vector by 26:
d=26⋅nunit=26⋅(12i−3j+4k13)
d=2613(12i−3j+4k)=2(12i−3j+4k)=24i−6j+8k
The vector of magnitude 26 units normal to the plane 12x−3y+4z=1 is:
d=24i−6j+8k
Topper's Solved these Questions
Similar Questions
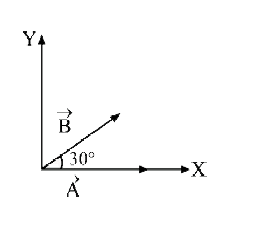
Vector →A of magnitude 4 units is directed along the positive x-axis. Another vector →B of magnitude 3 units lies in the x-y plane and is directed along 30∘ with the positive x-axis is as shown in figure. The magnitude of dot product →A.→B is:
View SolutionFind a vector →r of magnitude 3√2 units which makes an angle of π4 and π2 with y and z-axis respectively.
View SolutionFind the equation of planes parallel to the plane 2x−4y+4z=7 and which are at a distance of five units from the point (3,−1,2)
View SolutionFind the equation of the plane which is parallel to the plane x+5y−4z+5=0 and the sum of whose intercepts on the coordinate axes is 15 units.
View SolutionFind a normal vector to the plane x+2y+3z−6=0
View SolutionFind the equation of line of intersection of the planes 3x−y+z=1andx+4y−2z=2.
View SolutionFind the equations of the planes parallel to the plane x−2y+2z−3=0 which is at a unit distance from the point (1,2,3).
View SolutionWhat are the direction cosines of the normal to the plane 4x+12y+3z=65? Also find the lenth of perpendicular from the origin to the plane.
View SolutionFind the equations of the plane parallel to the plane x−2y+2z−3=0 and which are at a unit distance from the point (1, 1, 1).
View SolutionFind the reflection of the point (1, 2, −1) in the plane 3x−5y+4z=5.
View Solution
