Let d1, d2, d3 be three mutually exclusive diseases. Let S be the set of observable symptoms of these diseases. A doctor has the following information from a random sample of 5000 patients: 1800 had disease d1, 2100 has disease d2 and the others had disease d3. 1500 patients with disease d1, 1200 patients with disease d2 and 900 patients with disease d3 showed the symptom. Which of the diseases is the patient most likely to have?
To solve the problem, we will use Bayes' theorem to find the probability of each disease given the symptoms.
Step 1: Define Events
Let:
- E1: Event that a patient has disease d1
- E2: Event that a patient has disease d2
- E3: Event that a patient has disease d3
- A: Event that a patient shows symptoms
Step 2: Find the Total Number of Patients with Each Disease
From the problem:
- Total patients = 5000
- Patients with disease d1 = 1800
- Patients with disease d2 = 2100
- Patients with disease d3 = 5000−1800−2100=1100
Step 3: Find the Probability of Each Disease
The probabilities of each disease are:
- P(E1)=18005000=0.36
- P(E2)=21005000=0.42
- P(E3)=11005000=0.22
Step 4: Find the Probability of Symptoms Given Each Disease
From the problem:
- Patients with symptoms for disease d1 = 1500
- Patients with symptoms for disease d2 = 1200
- Patients with symptoms for disease d3 = 900
Thus, the probabilities are:
- P(A|E1)=15001800=56
- P(A|E2)=12002100=814=47
- P(A|E3)=9001100=911
Step 5: Apply Bayes' Theorem
Using Bayes' theorem:
P(Ei|A)=P(Ei)⋅P(A|Ei)P(E1)⋅P(A|E1)+P(E2)⋅P(A|E2)+P(E3)⋅P(A|E3)
Calculate P(E1|A):
P(E1|A)=P(E1)⋅P(A|E1)P(E1)⋅P(A|E1)+P(E2)⋅P(A|E2)+P(E3)⋅P(A|E3)
Substituting the values:
P(E1|A)=0.36⋅560.36⋅56+0.42⋅47+0.22⋅911
Calculate P(E2|A):
P(E2|A)=P(E2)⋅P(A|E2)P(E1)⋅P(A|E1)+P(E2)⋅P(A|E2)+P(E3)⋅P(A|E3)
Substituting the values:
P(E2|A)=0.42⋅470.36⋅56+0.42⋅47+0.22⋅911
Calculate P(E3|A):
P(E3|A)=P(E3)⋅P(A|E3)P(E1)⋅P(A|E1)+P(E2)⋅P(A|E2)+P(E3)⋅P(A|E3)
Substituting the values:
P(E3|A)=0.22⋅9110.36⋅56+0.42⋅47+0.22⋅911
Step 6: Calculate Each Probability
1. Calculate P(E1|A):
P(E1|A)=0.36⋅560.36⋅56+0.42⋅47+0.22⋅911≈0.4167
2. Calculate P(E2|A):
P(E2|A)=0.42⋅470.36⋅56+0.42⋅47+0.22⋅911≈0.3333
3. Calculate P(E3|A):
P(E3|A)=0.22⋅9110.36⋅56+0.42⋅47+0.22⋅911≈0.25
Step 7: Conclusion
Comparing the probabilities:
- P(E1|A)≈0.4167
- P(E2|A)≈0.3333
- P(E3|A)≈0.25
The disease the patient is most likely to have is d1 since P(E1|A) is the highest.
Let:
- E1: Event that a patient has disease d1
- E2: Event that a patient has disease d2
- E3: Event that a patient has disease d3
- A: Event that a patient shows symptoms
From the problem:
- Total patients = 5000
- Patients with disease d1 = 1800
- Patients with disease d2 = 2100
- Patients with disease d3 = 5000−1800−2100=1100
The probabilities of each disease are:
- P(E1)=18005000=0.36
- P(E2)=21005000=0.42
- P(E3)=11005000=0.22
From the problem:
- Patients with symptoms for disease d1 = 1500
- Patients with symptoms for disease d2 = 1200
- Patients with symptoms for disease d3 = 900
- P(A|E1)=15001800=56
- P(A|E2)=12002100=814=47
- P(A|E3)=9001100=911
Using Bayes' theorem:
P(Ei|A)=P(Ei)⋅P(A|Ei)P(E1)⋅P(A|E1)+P(E2)⋅P(A|E2)+P(E3)⋅P(A|E3)
P(E1|A)=P(E1)⋅P(A|E1)P(E1)⋅P(A|E1)+P(E2)⋅P(A|E2)+P(E3)⋅P(A|E3)
Substituting the values:
P(E1|A)=0.36⋅560.36⋅56+0.42⋅47+0.22⋅911
P(E2|A)=P(E2)⋅P(A|E2)P(E1)⋅P(A|E1)+P(E2)⋅P(A|E2)+P(E3)⋅P(A|E3)
Substituting the values:
P(E2|A)=0.42⋅470.36⋅56+0.42⋅47+0.22⋅911
P(E3|A)=P(E3)⋅P(A|E3)P(E1)⋅P(A|E1)+P(E2)⋅P(A|E2)+P(E3)⋅P(A|E3)
Substituting the values:
P(E3|A)=0.22⋅9110.36⋅56+0.42⋅47+0.22⋅911
1. Calculate P(E1|A):
P(E1|A)=0.36⋅560.36⋅56+0.42⋅47+0.22⋅911≈0.4167
P(E2|A)=0.42⋅470.36⋅56+0.42⋅47+0.22⋅911≈0.3333
P(E3|A)=0.22⋅9110.36⋅56+0.42⋅47+0.22⋅911≈0.25
Comparing the probabilities:
- P(E1|A)≈0.4167
- P(E2|A)≈0.3333
- P(E3|A)≈0.25
Topper's Solved these Questions
Similar Questions
A symptom of Graves' disease is
View SolutionMention three symptoms of the disease Hepatitis.
View SolutionLet d1,d2,d3 be thee mutually exclusive diseases. Let S={s1,s2,s3,,.....,s6} be the set of observable symptoms of these diseases. For example s1 is the shortness of breath, s2 is loss of weight, s3 is fatigue etc. Suppose a random sample of 10,000 patients contains 3200 patients with disease d1,3500 with disease d2and3300 with disease d3. Also, 3100 patients with disease d1,3300 with disease d2and3000 with disease d3 show the symptom S. Knowing that the patient has symptom S, the doctor wishes to determine the patients illness. One the basis of this information, what should the doctor conclude?
View SolutionGive the cause and one symptom of the following diseases:
ConstipationView Solutionacquired disease and congenital disease.
View SolutionSelect the symptoms of the disease caused by round worm
View SolutionSymptoms of red rot disease appear over
View SolutionA patient blood smear show the following picture. Which disease is the patient suffering from ?
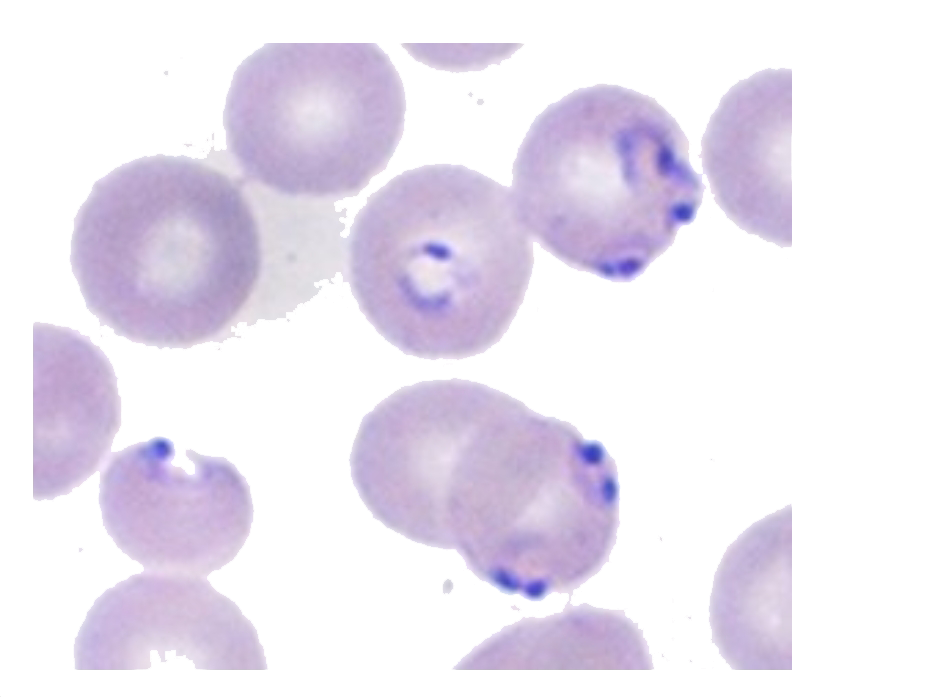 View Solution
View SolutionGive the cause and one symptom of the following diseases:
ArthritisView SolutionGive the cause and one symptom of following diseases.
UlcersView Solution

