State which of the following are not the probability distributions of a random variable. Give reasons for your answer.
To determine which of the given distributions are not probability distributions of a random variable, we need to check two main criteria for each distribution:
1. The sum of all probabilities must equal 1.
2. All probabilities must be non-negative (i.e., greater than or equal to 0).
Let's analyze each part step by step:
Step 1: Analyze the First Distribution
- Distribution:
- P(X = 1) = 0.4
- P(X = 2) = 0.4
- P(X = 3) = 0.2
- Sum of Probabilities:
- 0.4 + 0.4 + 0.2 = 1.0
- Conclusion:
- Since the sum of the probabilities equals 1 and all probabilities are non-negative, this is a valid probability distribution.
Step 2: Analyze the Second Distribution
- Distribution:
- P(X = 1) = -0.1 (negative probability)
- P(X = 2) = 0.5
- P(X = 3) = 0.6
- Conclusion:
- Since one of the probabilities is negative (P(X = 1) = -0.1), this is not a valid probability distribution.
Step 3: Analyze the Third Distribution
- Distribution:
- P(X = 1) = 0.6
- P(X = 2) = 0.1
- P(X = 3) = 0.2
- Sum of Probabilities:
- 0.6 + 0.1 + 0.2 = 0.9
- Conclusion:
- Since the sum of the probabilities does not equal 1 (it equals 0.9), this is not a valid probability distribution.
Step 4: Analyze the Fourth Distribution
- Distribution:
- P(X = 1) = 0.3
- P(X = 2) = 0.2
- P(X = 3) = 0.4
- P(X = 4) = 0.1
- P(X = 5) = 0.05
- Sum of Probabilities:
- 0.3 + 0.2 + 0.4 + 0.1 + 0.05 = 1.05
- Conclusion:
- Since the sum of the probabilities does not equal 1 (it equals 1.05), this is not a valid probability distribution.
Final Summary
- Valid Probability Distribution:
- First Distribution
- Not Valid Probability Distributions:
- Second Distribution (due to negative probability)
- Third Distribution (sum of probabilities not equal to 1)
- Fourth Distribution (sum of probabilities not equal to 1)
2. All probabilities must be non-negative (i.e., greater than or equal to 0).
- Distribution:
- P(X = 1) = 0.4
- P(X = 2) = 0.4
- P(X = 3) = 0.2
- 0.4 + 0.4 + 0.2 = 1.0
- Since the sum of the probabilities equals 1 and all probabilities are non-negative, this is a valid probability distribution.
- Distribution:
- P(X = 1) = -0.1 (negative probability)
- P(X = 2) = 0.5
- P(X = 3) = 0.6
- Since one of the probabilities is negative (P(X = 1) = -0.1), this is not a valid probability distribution.
- Distribution:
- P(X = 1) = 0.6
- P(X = 2) = 0.1
- P(X = 3) = 0.2
- 0.6 + 0.1 + 0.2 = 0.9
- Since the sum of the probabilities does not equal 1 (it equals 0.9), this is not a valid probability distribution.
- Distribution:
- P(X = 1) = 0.3
- P(X = 2) = 0.2
- P(X = 3) = 0.4
- P(X = 4) = 0.1
- P(X = 5) = 0.05
- 0.3 + 0.2 + 0.4 + 0.1 + 0.05 = 1.05
- Since the sum of the probabilities does not equal 1 (it equals 1.05), this is not a valid probability distribution.
- Valid Probability Distribution:
- First Distribution
- Not Valid Probability Distributions:
- Second Distribution (due to negative probability)
- Third Distribution (sum of probabilities not equal to 1)
- Fourth Distribution (sum of probabilities not equal to 1)
Topper's Solved these Questions
Similar Questions
Which of the following probability distribution does not exist for randam variable? Give reason?
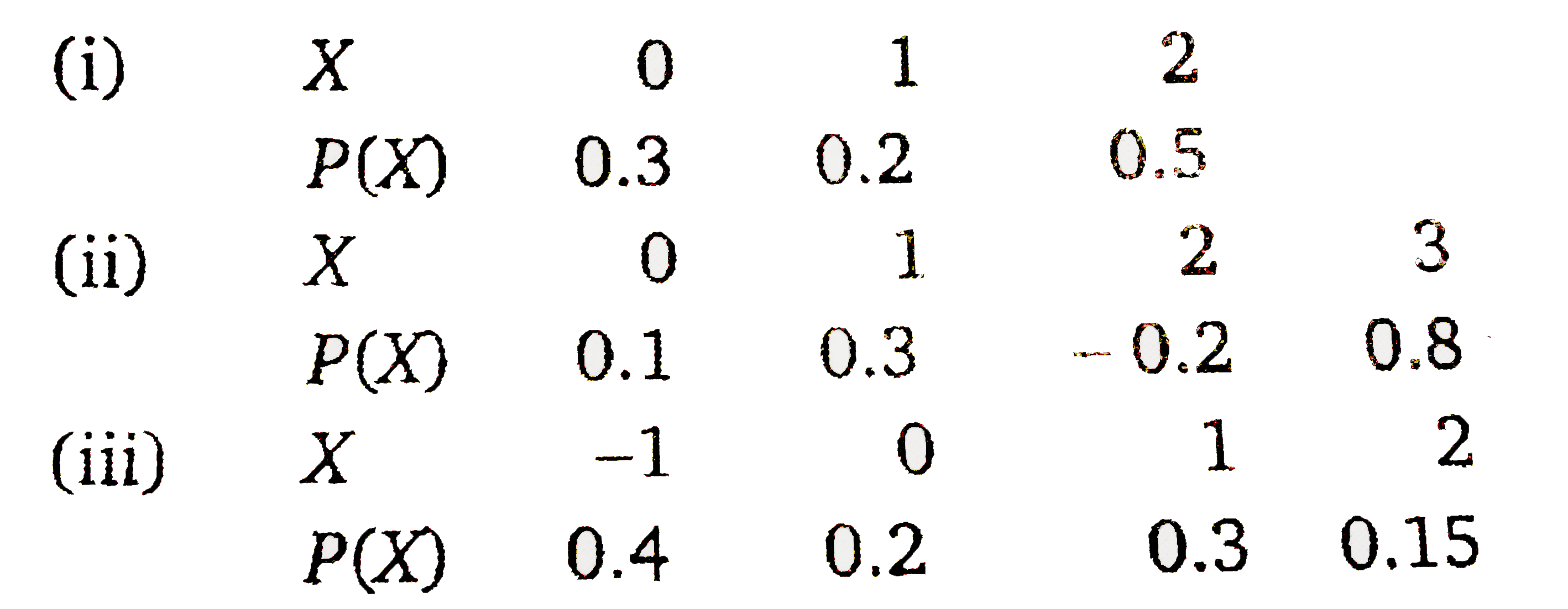
View SolutionThe following is the probability distribution of a random vaiable X.
The value of k is
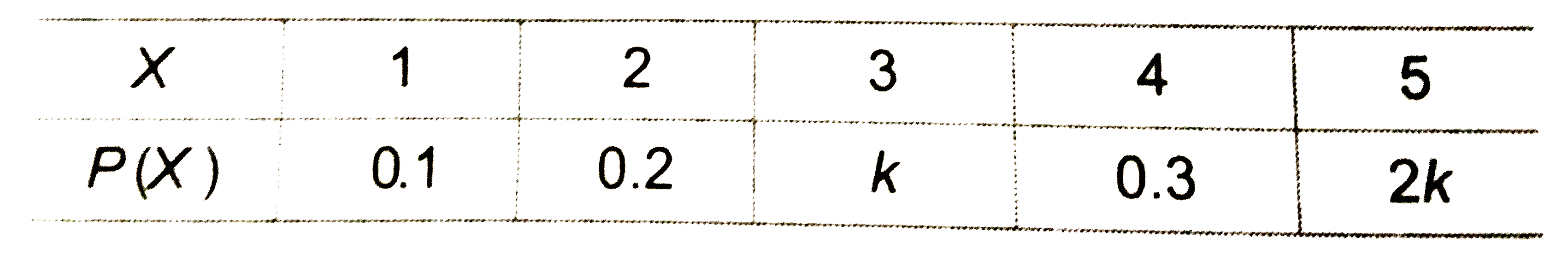
View SolutionConsider the probability distribution of a random variable X.

Variance of X
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View Solution
is the probability distribution of a random variable X. Find the variance of X.
View SolutionConsider the probability distribution of a random variable X.

V(X2)
View SolutionFind the value of k for probability distribution of a random variable X is give by:

View SolutionState whether the following probability distribution is admissible or not.

View SolutionState whether the following probability distribution is admissible or not.
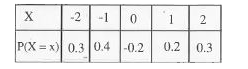
View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View Solution
