An office opens at 9 a.m. and closes at 5 p.m. with a lunch interval of 30 minutes. What is the ratio of lunch interval to the total period in office?
To find the ratio of the lunch interval to the total period in the office, we can follow these steps:
Step 1: Determine the total time period in the office.
The office opens at 9 a.m. and closes at 5 p.m.
- From 9 a.m. to 5 p.m., the total time is:
- 5 p.m. - 9 a.m. = 8 hours
Step 2: Convert the total time period from hours to minutes.
Since we need to compare the lunch interval (in minutes) to the total time period (also in minutes), we convert the total time period into minutes.
- We know that 1 hour = 60 minutes.
- Therefore, 8 hours = 8 × 60 = 480 minutes.
Step 3: Identify the lunch interval in minutes.
The lunch interval is given as 30 minutes.
Step 4: Set up the ratio of the lunch interval to the total time period.
Now we can set up the ratio of the lunch interval to the total time period.
- Lunch interval = 30 minutes
- Total time period = 480 minutes
The ratio is:
Ratio=Lunch IntervalTotal Time Period=30480
Step 5: Simplify the ratio.
To simplify the ratio, we can divide both the numerator and the denominator by their greatest common divisor (GCD), which is 30.
30÷30480÷30=116
Final Answer:
The ratio of the lunch interval to the total period in the office is 1:16.
---
The office opens at 9 a.m. and closes at 5 p.m.
- 5 p.m. - 9 a.m. = 8 hours
Since we need to compare the lunch interval (in minutes) to the total time period (also in minutes), we convert the total time period into minutes.
- Therefore, 8 hours = 8 × 60 = 480 minutes.
The lunch interval is given as 30 minutes.
Now we can set up the ratio of the lunch interval to the total time period.
- Total time period = 480 minutes
Ratio=Lunch IntervalTotal Time Period=30480
To simplify the ratio, we can divide both the numerator and the denominator by their greatest common divisor (GCD), which is 30.
The ratio of the lunch interval to the total period in the office is 1:16.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A man throws balls with the same speed vertically upwards one after the other at an interval of 2s. What should be the speed of the throw so that more than two balls are in the sky at any time ? (Given g=9.8m/s2)
AOnly with speed 19.6ms−1BMore than 19.6ms−1CAt least 9.8ms−1DAny speed less than 19.6ms−1A photocopy machine is initially loaded with 5,000 sheets of paper. The machine starts a large job and copies at a constant rate. After 20 minutes, it has used 30% of the paper. Which of the following equations models the number of sheets of paper, p, remaining in the machine m minutes after the machine started printing?
Ap = 5,000 − 20mBp = 5,000 − 75mCp=5,000(0.3)m20Dp=5,000(0.7)m20
A steel wire of length 4.7m and cross-section 3.0×10−5m2 stretched by the same amount as a copper wire of length 3.5m and cross-section 4.0×10−5m2 under a given load. What is the ratio of Young's modulus of steel to that of copper ?
View SolutionA steel wire of length 4.7 m and cross-section 3.0×102m2 stretches by the same amount as a copper wire of length 3.5 m and cross-section 4.0xx102m2 under a given load. What is the ratio of the Young.s modulus of steel to that of copper?
View SolutionConsider reaction in which reactant R is converted into product P: R→P. When the initial concentration of R′ is 0.5M The half life of the reaction is 20 minute. When the initial concentration is increased to 1.3 M, the half life decreases to 7.69 minute.
Q. What is the rate canstant of the reaction?
View SolutionA man starts from his home and walks 50 m towards, then he turns towards east and walks 40 m and then reaches to his office after moving 20 m towards south.
(i) What is the total distance covered by the man from his home to office ?
(ii) What is his displacement from his home to office ?
View Solution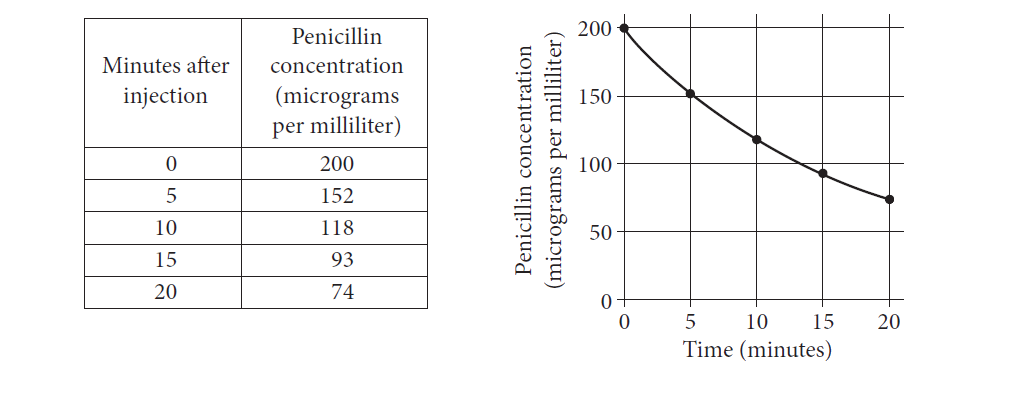
When a patient receives a penicillin injection, the kidneys begin removing the penicillin from the body. The table and graph above show the penicillin concentration in a patient’s bloodstream at 5 minute intervals for the 20 minutes immediately following a one-time penicillin injection.
The penicillin concentration, in micrograms per milliliter, in the patient’s bloodstream t minutes after the penicillin injection is modeled by the function P defined by P t = 200bt5 . If P approximates the values in the table to within 10 micrograms per milliliter, what is the value of b, rounded to the nearest tenth?
View SolutionA pipe of length 1.5 m closed at one end is filled with a gas and it resonates at 30∘C in its fundamental with a tuning fork. Another pipe of the same length but open at both ends and filled with air and it resonates in its fundamental with the same tuning fork. Calculate the velocity of sound at 0∘C in the gas, given that the velocity of sound in air is 360ms−1 at 30∘.
View Solution
