In each of the figures given below. Find x and y
To solve the problem of finding the values of x and y in the given figures, we will follow the steps outlined in the video transcript.
Step 1: Find x in the first figure.
- We know that x and 75∘ form a linear pair.
- The sum of angles in a linear pair is 180∘.
- Therefore, we can write the equation:
x+75∘=180∘
- To find x, we rearrange the equation:
x=180∘−75∘
- Calculating this gives:
x=105∘
Step 2: Find y in the first figure.
- We know that the sum of all angles in a triangle is 180∘.
- The angles in the triangle are y, 40∘, and 75∘.
- Therefore, we can write the equation:
y+40∘+75∘=180∘
- Simplifying the left side:
y+115∘=180∘
- To find y, we rearrange the equation:
y=180∘−115∘
- Calculating this gives:
y=65∘
Step 3: Find x in the second figure.
- Again, x and 80∘ form a linear pair.
- Therefore, we can write the equation:
x+80∘=180∘
- To find x, we rearrange the equation:
x=180∘−80∘
- Calculating this gives:
x=100∘
Step 4: Find y in the second figure.
- In this triangle, we have y, x (which we found to be 100∘), and 30∘.
- Therefore, we can write the equation:
y+x+30∘=180∘
- Substituting x=100∘:
y+100∘+30∘=180∘
- Simplifying the left side:
y+130∘=180∘
- To find y, we rearrange the equation:
y=180∘−130∘
- Calculating this gives:
y=50∘
Final Answers:
- For the first figure: x=105∘ and y=65∘
- For the second figure: x=100∘ and y=50∘
- We know that x and 75∘ form a linear pair.
- The sum of angles in a linear pair is 180∘.
- Therefore, we can write the equation:
x+75∘=180∘
- To find x, we rearrange the equation:
x=180∘−75∘
- Calculating this gives:
x=105∘
- We know that the sum of all angles in a triangle is 180∘.
- The angles in the triangle are y, 40∘, and 75∘.
- Therefore, we can write the equation:
y+40∘+75∘=180∘
- Simplifying the left side:
y+115∘=180∘
- To find y, we rearrange the equation:
y=180∘−115∘
- Calculating this gives:
y=65∘
- Again, x and 80∘ form a linear pair.
- Therefore, we can write the equation:
x+80∘=180∘
- To find x, we rearrange the equation:
x=180∘−80∘
- Calculating this gives:
x=100∘
- In this triangle, we have y, x (which we found to be 100∘), and 30∘.
- Therefore, we can write the equation:
y+x+30∘=180∘
- Substituting x=100∘:
y+100∘+30∘=180∘
- Simplifying the left side:
y+130∘=180∘
- To find y, we rearrange the equation:
y=180∘−130∘
- Calculating this gives:
y=50∘
- For the first figure: x=105∘ and y=65∘
- For the second figure: x=100∘ and y=50∘
Topper's Solved these Questions
Similar Questions
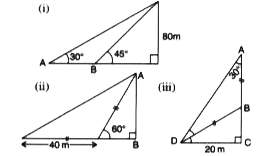
In the figures given below , find AB:
View SolutionFind the area of the figure given below.

View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons

View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons

View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons
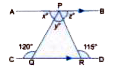
View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons
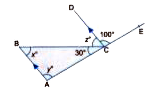
View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons
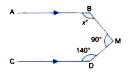
View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons

View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons

View SolutionIn each of the figures given below, AB∣∣CD. Find the unknown angles, giving reasons
View Solution
