Calculate the area of the pentagon , where and with dimensions as shown in Fig.36.
Step by step video & image solution for Calculate the area of the pentagon A B C D E , where A B=A E and with dimensions as shown in Fig.36. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Calculate the area of the quadrilateral ABCD as shown in Fig.33, given that BD=42 cm , AC=28 cm , OD=12 cm and AC⊥BD .
View SolutionCalculate the area of quadrilateral field ABCD as shown in Fig.35, by dividing it into a rectangle and a triangle.
View SolutionTwo equal chords AB and CD of a circle with centre O , when produced meet at a point E, as shown in Figure. Prove that BE=DE and AE=CE.
View SolutionTwo equal chords AB and CD of a circle with centre O, when produced meet at a point E, as shown in Figure. Prove that BE=DE and AE=CE.
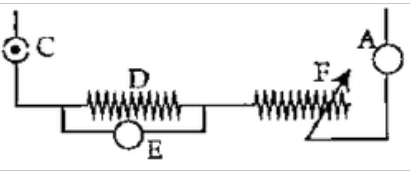
View SolutionIn the electric circuit shown in Fig., label the parts A, B, C, D, E, and E
State the function of each part. Show in the diagram the direction of flow of current.
View SolutionTwo equal chords AB and CD of a circle with centre O , when produced meet at a point E, as shown in Figure, Prove that BE=DE and AE=CE.
View SolutionIn Fig. 4.178, DE∥BC (FIGURE) (i) If DE=4cm , BC=6cm and Area (ADE)=16 cm2 , find the area of ABC . (ii) If DE=4cm, BC=8cm and Area (ADE)=25 cm2 , find the area of ABC . (iii) If DE:BC=3:5 . Calculate the ratio of the areas of ADE and the trapezium BCED .
View SolutionParallelogram ABCD and rectangle ABEF have the same base AB and also have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle. GIVEN : A∣∣gmABCD and a rectangle ABEF with the same base AB and equal areas. TO PROVE : Perimeter of ∣∣gmABCD > Perimeter of rectangle ABEF i.e. AB+BC+CD+AD>AB+BE+EF+AF
View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC . Prove that DF⋅EF=FB⋅FA.
View SolutionFind the area of the pentagon whose vertices are A(1,1),B(7,21),C(7,−3),D(12,2), and E(0,−3)
View Solution
