For any two rational numbers a and b, a5x b5
is equal to
(a x b)0
(b) (a x b)10
(c)
(a x b)5
(d) (a x b)25
To solve the question, we need to simplify the expression a5×b5 using the properties of exponents.
1. Identify the Expression: We start with the expression a5×b5.
2. Apply the Property of Exponents: We use the property of exponents which states that xm×ym=(x×y)m. Here, x is a, y is b, and m is 5.
3. Rewrite the Expression: According to the property, we can rewrite the expression as:
a5×b5=(a×b)5
4. Conclusion: Therefore, the expression a5×b5 simplifies to (a×b)5.
5. Select the Correct Option: From the options provided, the correct answer is:
(a×b)5(Option C)
Final Answer:
The answer is (a×b)5 (Option C).
---
a5×b5=(a×b)5
(a×b)5(Option C)
The answer is (a×b)5 (Option C).
Topper's Solved these Questions
Similar Questions
a2b3 × 2ab2 is equal to: (a) 2a3b4 (b) 2a3b5 (c) 2ab (d) a3b5
View Solution4 a 2 b 3 x 3a b 2 x 5 a 3 b is equal to: (a) 60 a 3 b 5 (b) 60 a 6 b 5 (c) 60 a 6 b 6 (d) a 6 b 5
View Solutiona3x2a2bx3ab5 is equal to:
(a)a6b6
(b) 23a6b6
(c) 6a6b6
(d) None of these
View SolutionIf a, b, c are positive real numbers, then 5√3125 a10b5c10 is equal to
(a) 5a2bc2
(b) 25ab2c
(c) 5a3bc3
(d) 125 a2bc2
View SolutionFor any positive real number x, find the value of (xaxb)a+b × (xbxc)b+c × (xcxa)c+a
View SolutionLet a,b,c be rational numbers and f:Z→Z be a function given by f(x)=ax2+bx+c. Then, a+b is
View SolutionIf x+2 is a factor of x2+ax+2b and a+b=4, then (a) a=1, b=3 (b) a=3, b=1 (c) a=−1, b=5 (d) a=5, b=−1
View SolutionAssuming that x is a positive real number and a, b, c are rational numbers, show that: (xaxb)a+b (xbxc)b+c(xcxa)c+a=1
View SolutionAssuming that x is a positive real number and a, b, c are rational numbers, show that: (xaxb)1ab (xbxc)1bc (xcxa)1ac=1
View SolutionIn the figure, if AB=AC,∠BAD=300 and AE=AD, then x is equal to
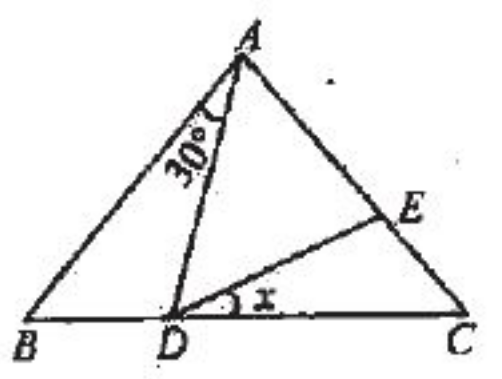
a)150 (b) 100 (c) 12.50 (d) 7.50
View Solution
