Find the constant of variation from the table given below: x, 3, 5, 7, 9 y, 12, 20, 28, 36 set up table and solve the following problems .
To find the constant of variation from the given table of values, we will follow these steps:
Step 1: Set Up the Table
We will create a table with the given values of x and y.
| x | y |
|-------|-------|
| 3 | 12 |
| 5 | 20 |
| 7 | 28 |
| 9 | 36 |
Step 2: Use the Formula for Direct Variation
In direct variation, the relationship between x and y can be expressed as:
y=kx
where k is the constant of variation.
Step 3: Find the Constant of Variation for Each Pair
We will calculate k for each pair of x and y using the formula:
k=yx
For the first pair (3,12):
k=123=4
For the second pair (5,20):
k=205=4
For the third pair (7,28):
k=287=4
For the fourth pair (9,36):
k=369=4
Step 4: Conclusion
From all the calculations, we can see that the constant of variation k is the same for all pairs:
k=4
Thus, the constant of variation from the table is 4.
---
We will create a table with the given values of x and y.
|-------|-------|
| 3 | 12 |
| 5 | 20 |
| 7 | 28 |
| 9 | 36 |
In direct variation, the relationship between x and y can be expressed as:
y=kx
where k is the constant of variation.
We will calculate k for each pair of x and y using the formula:
k=yx
k=123=4
k=205=4
k=287=4
k=369=4
From all the calculations, we can see that the constant of variation k is the same for all pairs:
k=4
Topper's Solved these Questions
Similar Questions
IF p and q are in direct variation of x, y and z in the table given below:
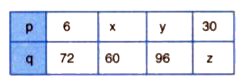
View Solution. Find the median of the given data:
8, 9, 12, 7, 5, 4, 18, 20, 6,3
View SolutionSolve the following: 7.5−3.6−(3.9−6.3)
View SolutionSuggest a universal set for the sets given below :
(5,7,9) , (3,5,7) ,(1,3,9) and ( 2,4,8)
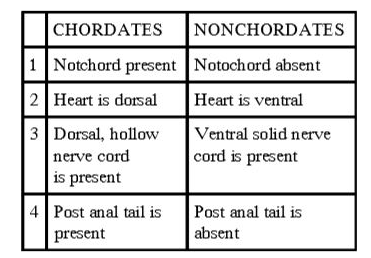
View SolutionFind out the wrong difference between chordates and nonchordates from the table given below :-
View SolutionIn which of the following tables, a and b vary directly. Also, find the constant of variation if a and b are in direct variation. (i) a: 4, 7, 21, 28 and b:12, 21, 63, 84 (ii) a: 2.5, 5, 7.5, 10, 15 and b:10, 20, 30, 40, 60 (iii) a:1, 2, 3, 4, 5 and b:2, 1, 6, 3, 2/5
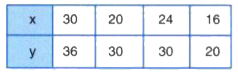
View SolutionFrom tha table given below find whether x and y in direct proporation or not.
View SolutionFrom the list below, form 10 pairs of co-prime numbers: 3, 5, 8, 9, 12, 15, 16, 28
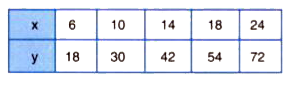
View SolutionObserve the table given below and find whether x and y are in direct variations or not :
View SolutionFind the 12th term from the end of the following arithmetic progression: 3,5,7,9…..201
View Solution
