In Figure, RICE is parallelogram. Find x, y, z.
To solve the problem, we need to find the values of x, y, and z in the parallelogram RICE.
1. Understanding the Properties of Parallelograms:
- In a parallelogram, the diagonals bisect each other. This means that the segments formed by the diagonals are equal.
2. Identify Given Values:
- We are given the lengths:
- RE=13
- OI=5
- OC=12
3. Using the Properties of the Parallelogram:
- Let O be the point where the diagonals intersect.
- Since OI and OE are equal (because diagonals bisect each other), we have:
OE=OI=5
- Therefore, we can conclude:
x=OE=5
4. Finding the Value of y:
- Similarly, since OR and OC are equal, we have:
OR=OC=12
- Thus, we can conclude:
y=OR=12
5. Finding the Value of z:
- We need to find z using the Pythagorean theorem in triangle OIR since it is a right triangle:
IR2=OR2+OI2
- Substituting the values of OR and OI:
z2=y2+OI2
z2=122+52
- Calculating the squares:
z2=144+25
z2=169
- Taking the square root to find z:
z=√169=13
6. Final Values:
- Thus, we have:
x=5,y=12,z=13
Summary of Results:
- x=5
- y=12
- z=13
- In a parallelogram, the diagonals bisect each other. This means that the segments formed by the diagonals are equal.
- We are given the lengths:
- RE=13
- OI=5
- OC=12
- Let O be the point where the diagonals intersect.
- Since OI and OE are equal (because diagonals bisect each other), we have:
OE=OI=5
- Therefore, we can conclude:
x=OE=5
- Similarly, since OR and OC are equal, we have:
OR=OC=12
- Thus, we can conclude:
y=OR=12
- We need to find z using the Pythagorean theorem in triangle OIR since it is a right triangle:
IR2=OR2+OI2
- Substituting the values of OR and OI:
z2=y2+OI2
z2=122+52
- Calculating the squares:
z2=144+25
z2=169
- Taking the square root to find z:
z=√169=13
- Thus, we have:
x=5,y=12,z=13
- x=5
- y=12
- z=13
Topper's Solved these Questions
Similar Questions
In Figure, BEST is a parallelogram. Find the values of x, y and z.
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram. Figure
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid-points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
View SolutionIn Figure, ABCD is a parallelogram. Find the values of xandy.
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX (iii) AYB ≅CXD (iv) AXD≅ CYB
View SolutionIn Figure, ABCD is a parallelogram and EFCD is a rectangle. Also AL ⊥DC. Prove that
(i) ar(ABCD=ar(EFCD)
(ii) ar (ABCD)=DC x AL
View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
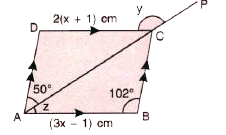
View SolutionIn Figure, RING is a parallelogram, if ∠R=700, find all other angles.
View SolutionIn the adjacent figure HOPE is a parallelogram. Find the angle measures x, y and Z. State the geometrical truths you use to find them. (Figure)
View Solution
