A plot is in the form of a rectangle ABCD having semi-circle on BC as shown in Figure. If AB=60m and BC=28cm, find the area of the plot.
To find the area of the plot in the form of a rectangle with a semicircle on one of its sides, we can follow these steps:
Step 1: Identify the dimensions of the rectangle and semicircle
- The length of side AB (the length of the rectangle) is given as 60 meters.
- The length of side BC (the width of the rectangle) is given as 28 centimeters.
Step 2: Convert all measurements to the same unit
- Since AB is in meters and BC is in centimeters, we need to convert BC to meters for consistency.
BC=28 cm=28100 m=0.28 m
Step 3: Calculate the radius of the semicircle
- The semicircle is on side BC, so the radius r of the semicircle is half of BC.
r=BC2=0.282=0.14 m
Step 4: Calculate the area of the rectangle
- The area Arectangle of the rectangle can be calculated using the formula:
Arectangle=AB×BC=60 m×0.28 m=16.8 m2
Step 5: Calculate the area of the semicircle
- The area Asemicircle of the semicircle can be calculated using the formula:
Asemicircle=12πr2
Substituting r=0.14 m:
Asemicircle=12×227×(0.14)2
=12×227×0.0196≈0.0308 m2
Step 6: Calculate the total area of the plot
- The total area Atotal of the plot is the sum of the area of the rectangle and the area of the semicircle.
Atotal=Arectangle+Asemicircle=16.8 m2+0.0308 m2≈16.8308 m2
Step 7: Round the final answer
- Rounding the total area to two decimal places:
Atotal≈16.83 m2
Final Answer
The area of the plot is approximately 16.83 m².
---
- The length of side AB (the length of the rectangle) is given as 60 meters.
- The length of side BC (the width of the rectangle) is given as 28 centimeters.
- Since AB is in meters and BC is in centimeters, we need to convert BC to meters for consistency.
BC=28 cm=28100 m=0.28 m
- The semicircle is on side BC, so the radius r of the semicircle is half of BC.
r=BC2=0.282=0.14 m
- The area Arectangle of the rectangle can be calculated using the formula:
Arectangle=AB×BC=60 m×0.28 m=16.8 m2
- The area Asemicircle of the semicircle can be calculated using the formula:
Asemicircle=12πr2
Substituting r=0.14 m:
Asemicircle=12×227×(0.14)2
=12×227×0.0196≈0.0308 m2
- The total area Atotal of the plot is the sum of the area of the rectangle and the area of the semicircle.
Atotal=Arectangle+Asemicircle=16.8 m2+0.0308 m2≈16.8308 m2
- Rounding the total area to two decimal places:
Atotal≈16.83 m2
The area of the plot is approximately 16.83 m².
Topper's Solved these Questions
- LINEAR EQUATION IN ONE VARIABLEBOOK - RD SHARMA ENGLISHCHAPTER - LINEAR EQUATION IN ONE VARIABLEEXERCISE - All Questions
110 Videos
- MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)BOOK - RD SHARMA ENGLISHCHAPTER - MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)EXERCISE - All Questions
134 Videos
Similar Questions
A plot is in the form of a rectangle ABCD having semi-circle on BC as shown in Fig. 15.64. If AB=60 m and BC=28 m , find the area of the plot. (FIGURE)
View SolutionIn Figure, BD=DC and ∠DBC=250 find the measure of ∠BAC
View SolutionIn Figure, if ∠BAC=600 and ∠BCA=200, find ∠ADC
View SolutionTwo concentric circle with centre O have A, B, C, D as the points of intersection with the line l as shown in Figure. If AD=12cm and BC=8cm, find the lengths of AB, CD, AC and BD.
View SolutionA sheet of paper is in the form of a rectangle ABCD in which AB=40cm and AD=28cm . A semi-circular portion with BC as diameter is cut off. Find the area of the remaining paper.
View SolutionA paper is in the form of a rectangle ABCD in which AB=20 cm and BC=14 cm. A semicircular portion with BC as diameter is cut off. Find the area of the remaining part.
View SolutionA paper is in the form of a rectangle ABCD in which AB=20cm and BC=14cm. A semi-circular portion with BC as diameter is cut off. Find the area of remaining part.
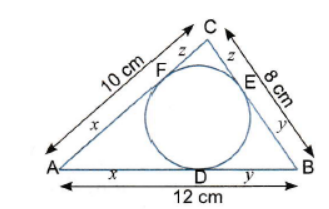
View SolutionA circle is inscribed in a ABC having side 8cm,10cmand12cm as shown in Figure. Find AD,BEandCF.
View SolutionIn Figure, ABCD is a rectangle with sides AB=10cm and AD=5cm. Find the area of EFG
View SolutionIn Figure, ABCD is a rectangle with sides AB=10cm and AD=5cm. Find the area of EFG
View Solution
