A rectangular strip 25cm x 7cm is rotated about the longer side. Find the total surface area of the solid thus generated.
To find the total surface area of the solid generated by rotating a rectangular strip of dimensions 25 cm x 7 cm about its longer side, we can follow these steps:
Step 1: Identify the dimensions
The dimensions of the rectangular strip are:
- Length (h) = 25 cm (this will be the height of the cylinder)
- Width = 7 cm (this will be used to find the radius of the cylinder)
Step 2: Determine the height and circumference
When the strip is rotated about its longer side (the 25 cm side), the height of the resulting cylinder is:
- Height (h) = 25 cm
The width of the strip becomes the circumference of the cylinder:
- Circumference (C) = 7 cm
Step 3: Relate circumference to radius
The circumference of a cylinder is given by the formula:
C=2πr
where r is the radius. We can rearrange this formula to find the radius:
r=C2π
Step 4: Calculate the radius
Substituting the value of the circumference:
r=72π
Using π≈227:
r=72×227
r=7×72×22
r=4944
r≈1.11cm
Step 5: Calculate the total surface area
The total surface area (TSA) of a cylinder is given by the formula:
TSA=2πr(r+h)
Substituting the values of r and h:
TSA=2π(4944)(4944+25)
Calculating 4944+25:
4944+25=49+110044=114944
Now substituting back into the TSA formula:
TSA=2×227×4944×114944
Calculating this gives:
TSA≈182.17cm2
Final Answer:
The total surface area of the solid generated is approximately 182.17 cm².
---
The dimensions of the rectangular strip are:
- Length (h) = 25 cm (this will be the height of the cylinder)
- Width = 7 cm (this will be used to find the radius of the cylinder)
When the strip is rotated about its longer side (the 25 cm side), the height of the resulting cylinder is:
- Height (h) = 25 cm
- Circumference (C) = 7 cm
The circumference of a cylinder is given by the formula:
C=2πr
where r is the radius. We can rearrange this formula to find the radius:
r=C2π
Substituting the value of the circumference:
r=72π
r=72×227
r=7×72×22
r=4944
r≈1.11cm
The total surface area (TSA) of a cylinder is given by the formula:
TSA=2πr(r+h)
TSA=2π(4944)(4944+25)
4944+25=49+110044=114944
TSA=2×227×4944×114944
TSA≈182.17cm2
The total surface area of the solid generated is approximately 182.17 cm².
Topper's Solved these Questions
Similar Questions
The sides containing right angle of a right angled triangle are 8 cm and 6 cm. It is rotated about the side of 8 cm. Find the total surface area of the formed solid.
View SolutionThe sides containing right angles of a right angled triangle are 8 cm and 6 cm it is rotated about its hypotenuse . Find the volume and total surface area of the solid formed.
View Solution
Knowledge Check
A rectangular park is 25 m long and 15 m wide. A path 3 m is constructed outside the park. Find the area of the path.
A277m2B276m2C266m2D256m2
A right angled triangle of which the sides containing the right angle are 6.3 cm and 10cm in length, is made to turn round on the longer side. Find the volume of the solid, thus generated. Also, find its curved surface area.
View SolutionThe sides containing right angles of a right angled triangle are 8 cm and 6 cm. It is rotated about its hypotenus. Find the volume and total surface area of the formed solid.
View SolutionA semi-circle of radius 17.5 cm is rotated about its diameter. Find the curved surface of so generated solid.
View SolutionFind the surface area of a cube whose edge is 11 cm
View SolutionA solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
View SolutionThe measure of angle angle QPR is 90 degrees, and the area of triangle PQR is 6. If triangle PQR is rotated 360∘ about side PR, what is the total surface area of the resulting solid ?
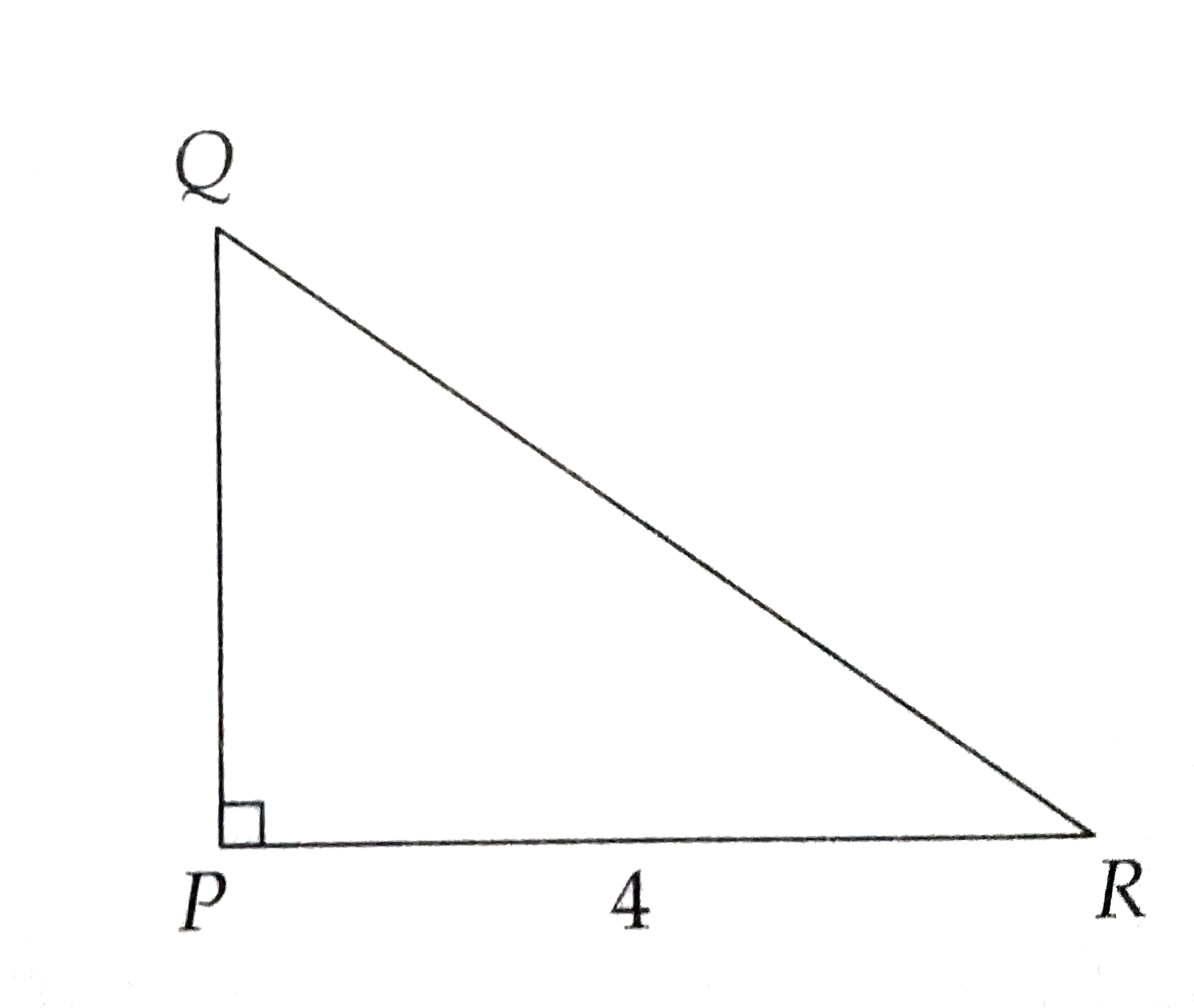
View SolutionA solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid (Use π=22/7 )
View Solution