A particle is projected horizontally with a speed $u$ from the top of plane inclined at an angle $θ$ with the horizontal. How far from the point of projection will the particle strike the plane ?

Video Solution

Text Solution

Verified by Experts

Take X,Y-axis as shown in ure Suppose that the particle strikes the plane at a point P with coordiN/Ates (x,y). Consider the motion between A and P.

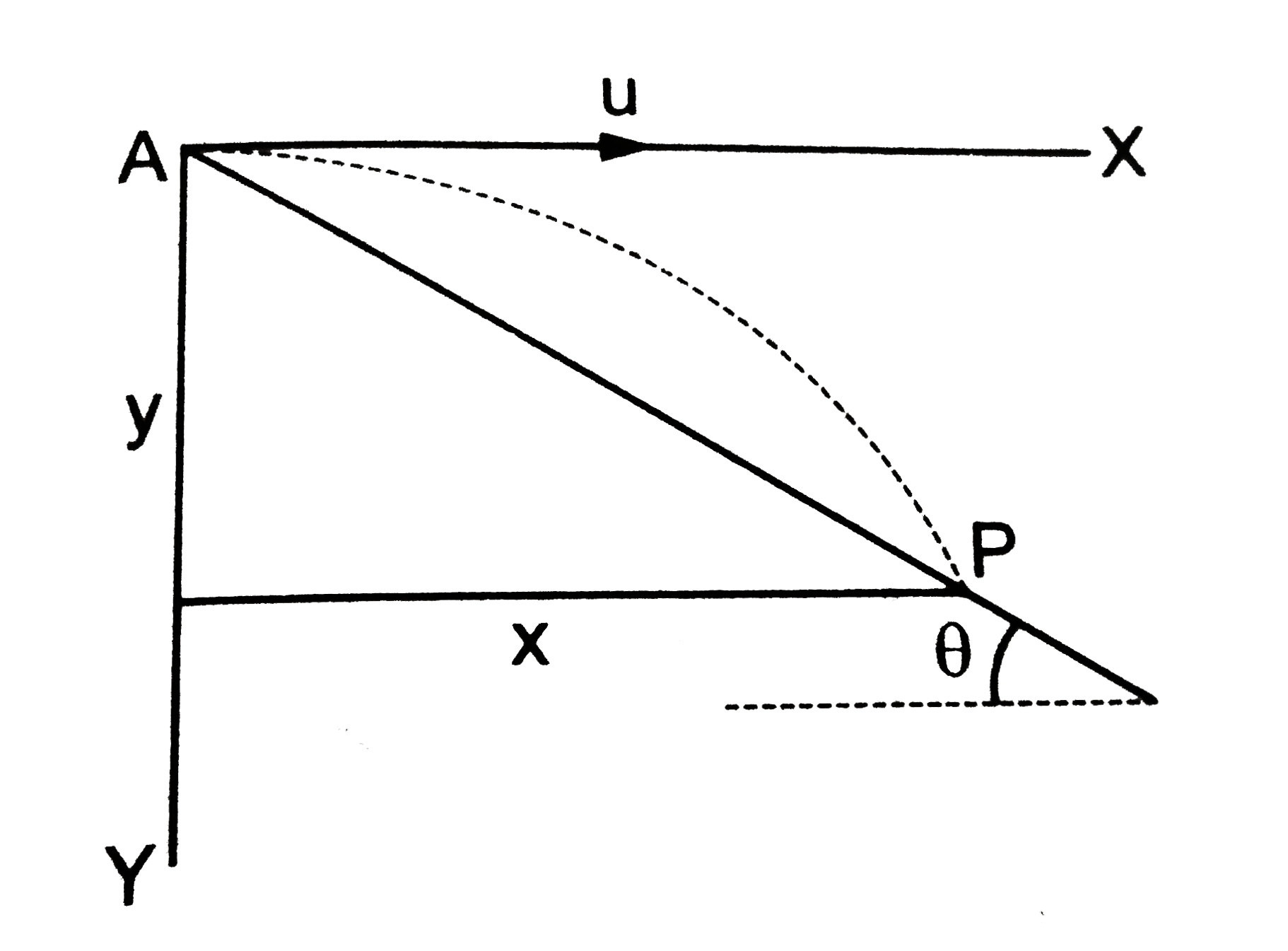
Motion in x- direction
$I n i t i a l v e l o c i t y = u$
$A e \leq r a t i o n = g$
$y = \frac{1}{2} >^{2}$
ElimiN/Ating t from i. and ii
$y = \frac{1}{2} g \frac{x^{2}}{u^{2}}$
Also $y = x tan θ$
$T h u s,$ (gx^2)/(2u^2)=x tan theta $g i v \in g$ x=0, or, $\frac{2 u^{2} tan θ}{g}, < b r > t h e n$ y= x tantheta= (2u^2 tan^2 theta)/g $< b r > T h e d i s tan c e$ AP=l=sqrt(x^2+y^2) $< b r >$ =(2u^2)/g tan theta sqrt (1+tan^2theta) $< b r >$ =(2u^2)/g tantheta sec theta. $A < e r \frac{N}{A} t i v e l y : T a k e t h e a x e s a s s h o w n \in u r e . c o n s r t h e m o t i o n b e t w e e n A and P . < b r > < i m g a \leq ocr_image l o a d \in g = lazy s r c = https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C03_S01_024_S02.png w h = 80% mx-auto s t y \leq = background:white; > < b r > M o t i o n a l o n g t h e X - a ξ s : < b r > I n t i a l v e l o c i t y$ =u cos theta $< b r > A e \leq r a t i o n$ =g sin theta $< b r >$ Displacement =AP $. < b r > T h u s,$ AP=(u cos theta)t+1/2(g sin theta)t^2 $< b r > M o t i o n a l o n g t h e Y - a ξ s < b r >$ Initial velocity =-u sin theta $< b r >$ acceleration =g cos theta $< b r >$ Displacement =0 $< b r > T h u s,$ 0=- uy sin theta +1/2 gt^2 cos theta $< b r >$ or, $t = 0, \frac{2 u sin θ}{g (cos θ)}$
clearly the point P corresponds to $t = \frac{2 u sin θ}{g cos θ}$
Putting this value of t in i.
$A P = (u cos θ) (\frac{2 u sin θ}{g cos θ}) + \frac{g sin θ}{2} {(\frac{2 u sin θ}{g cos θ})}^{2}$
$\frac{2 u^{2} sin θ}{g} + \frac{2 u^{2} sin θ {tan}^{2} θ}{g}$
$= \frac{2 u^{2}}{g} sin θ {sec}^{2} θ = \frac{2 u^{2}}{g} tan θ sec θ$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

HC VERMA ENGLISH-REST AND MOTION : KINEMATICS-worked out Examples

Home
Ask Doubt
Profile