A car travelling at 60 km/h overtakes another car travelling at 42 km/h. Assuming each car to be 5.0 m long, find the time taken during the overtake and the total road distance used for the overtake.
To solve the problem, we will follow these steps:
Step 1: Convert the speeds from km/h to m/s
The speeds of the cars are given in kilometers per hour (km/h). We need to convert them to meters per second (m/s) using the conversion factor:
1 km/h=518 m/s
For car A (60 km/h):
Speed of car A=60×518=30018=503 m/s
For car B (42 km/h):
Speed of car B=42×518=21018=353 m/s
Step 2: Calculate the relative velocity of car A with respect to car B
The relative velocity is calculated by subtracting the speed of car B from the speed of car A:
Relative velocity=Speed of car A−Speed of car B=503−353=153=5 m/s
Step 3: Calculate the total distance to be covered during the overtake
To overtake, car A must cover the length of both cars (5 m + 5 m):
Total distance=5 m+5 m=10 m
Step 4: Calculate the time taken to overtake
Using the formula:
Time=DistanceRelative Velocity
Substituting the values:
Time=10 m5 m/s=2 seconds
Step 5: Calculate the distance traveled by car A during the overtaking time
Using the speed of car A, we can find the distance traveled during the overtaking time:
Distance traveled by car A=Speed of car A×Time=503 m/s×2 s=1003 m≈33.33 m
Step 6: Calculate the total road distance used for the overtake
The total distance used for the overtake includes the distance traveled by car A plus the length of car A:
Total road distance=Distance traveled by car A+Length of car A=1003 m+5 m=1003+153=1153 m≈38.33 m
Final Answers:
- Time taken during the overtake: 2 seconds
- Total road distance used for the overtake: approximately 38.33 meters
The speeds of the cars are given in kilometers per hour (km/h). We need to convert them to meters per second (m/s) using the conversion factor:
1 km/h=518 m/s
Speed of car A=60×518=30018=503 m/s
Speed of car B=42×518=21018=353 m/s
The relative velocity is calculated by subtracting the speed of car B from the speed of car A:
Relative velocity=Speed of car A−Speed of car B=503−353=153=5 m/s
To overtake, car A must cover the length of both cars (5 m + 5 m):
Total distance=5 m+5 m=10 m
Using the formula:
Time=DistanceRelative Velocity
Substituting the values:
Time=10 m5 m/s=2 seconds
Using the speed of car A, we can find the distance traveled during the overtaking time:
Distance traveled by car A=Speed of car A×Time=503 m/s×2 s=1003 m≈33.33 m
The total distance used for the overtake includes the distance traveled by car A plus the length of car A:
Total road distance=Distance traveled by car A+Length of car A=1003 m+5 m=1003+153=1153 m≈38.33 m
- Time taken during the overtake: 2 seconds
- Total road distance used for the overtake: approximately 38.33 meters
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -29videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
Similar Questions
A car 2 m long travelling at 30ms−1 overtakes another car 4 m long travelling at 20ms−1. The time taken by the first car to pass the second car is
View Solution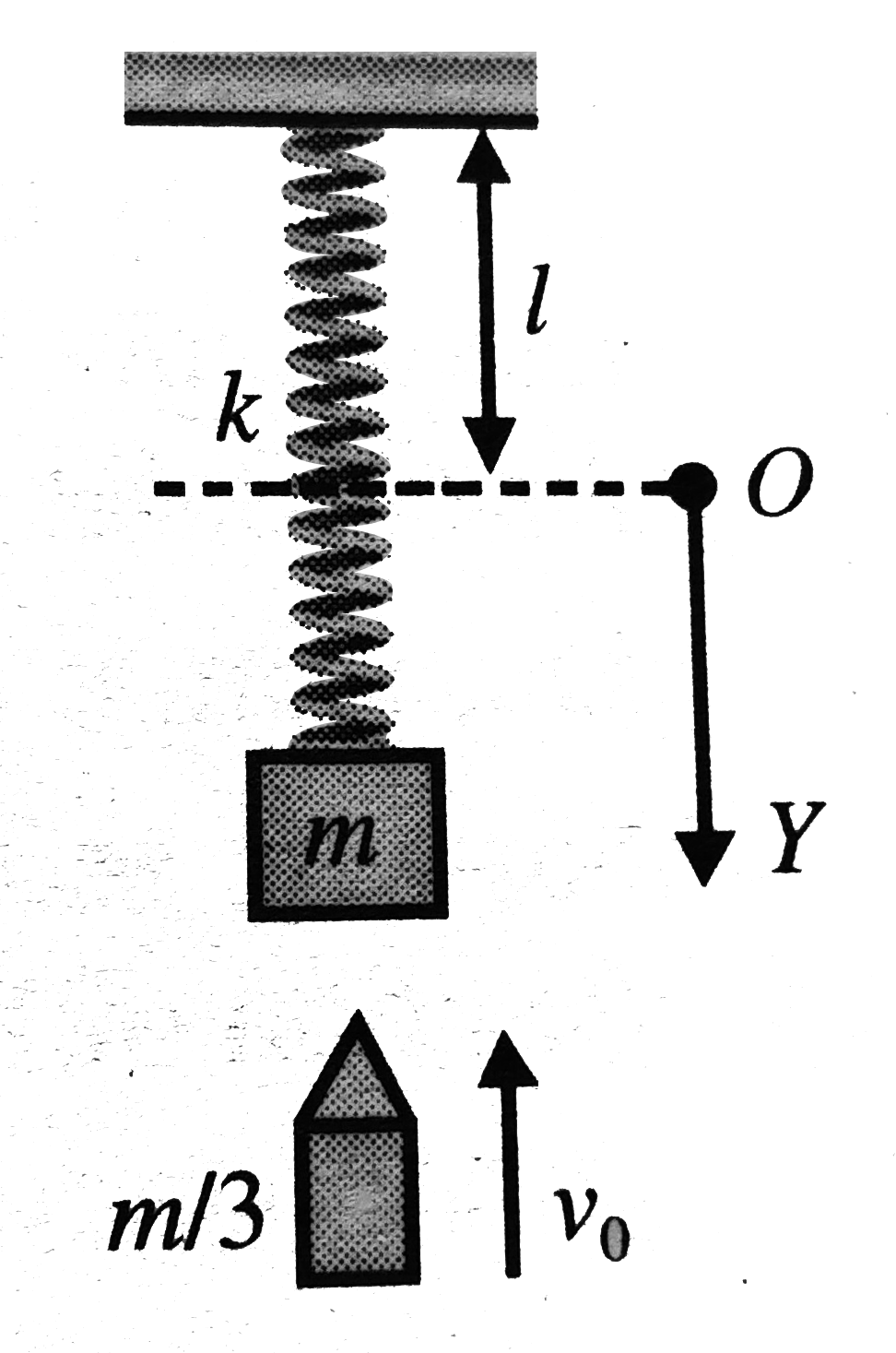
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)View SolutionA train of length 200 m traveling at 30ms−1 overtakes another train of length 300 m traveling at 20ms−1. The time taken by the first train to pass the second is
View SolutionA train 100m long travelling at 40ms−1 starts overtaking another train 200m long travelling at 30ms−1. The time taken by the forst train to pass the second train comletely is .
View SolutionA car travelling with a velocity of 80 km/h slowed down to 44 km/h in 15 s. The retardation is
View SolutionA car travelling with a velocity of 80 km/h slowed down to 44 km/h in 15 s. The retardation is
View SolutionA car travelling with a velocity of 80 km/h slowed down to 40 km/h in 10s. The retardation is
View SolutionA car trvelling at 108kmh−1 has its speed reduced to 36kmh−1 after traelling a distance of 2000m Find the retardation (assumed uniform) and time taken for this process.
View SolutionA car travels 165 km in 3 hours.
How long will it take to travel 440 km?View SolutionA car travels for 20 min with a constant speed of 54 km h−1 Find the distance travelled by the car.
View Solution

