A boy is sitting on a chair placed on the floor of a room. Write as many action reaction pairs of forces as you can.
To analyze the situation of a boy sitting on a chair, we can identify several action-reaction pairs of forces based on Newton's Third Law of Motion, which states that for every action, there is an equal and opposite reaction. Here’s a step-by-step breakdown of the action-reaction pairs:
Step 1: Boy Exerting Force on Chair
- Action: The boy exerts a downward force on the chair due to his weight, which is equal to mg (where m is the mass of the boy and g is the acceleration due to gravity).
- Reaction: The chair exerts an equal and opposite force upward on the boy, which is also mg.
Step 2: Chair Exerting Force on the Floor
- Action: The chair, along with the boy sitting on it, exerts a downward force on the floor due to their combined weight, which is (M+m)g (where M is the mass of the chair).
- Reaction: The floor exerts an equal and opposite force upward on the chair, which is also (M+m)g.
Step 3: Earth Exerting Force on Chair
- Action: The chair exerts a downward gravitational force on the Earth due to its weight, which is (M+m)g.
- Reaction: The Earth exerts an equal and opposite force upward on the chair.
Step 4: Boy Exerting Force on Earth
- Action: The boy exerts a downward gravitational force on the Earth due to his weight, which is mg.
- Reaction: The Earth exerts an equal and opposite force upward on the boy.
Summary of Action-Reaction Pairs
1. Boy → Chair: Downward force mg (Action)
- Chair → Boy: Upward force mg (Reaction)
2. Chair → Floor: Downward force (M+m)g (Action)
- Floor → Chair: Upward force (M+m)g (Reaction)
3. Chair → Earth: Downward force (M+m)g (Action)
- Earth → Chair: Upward force (M+m)g (Reaction)
4. Boy → Earth: Downward force mg (Action)
- Earth → Boy: Upward force mg (Reaction)
- Action: The boy exerts a downward force on the chair due to his weight, which is equal to mg (where m is the mass of the boy and g is the acceleration due to gravity).
- Reaction: The chair exerts an equal and opposite force upward on the boy, which is also mg.
- Action: The chair, along with the boy sitting on it, exerts a downward force on the floor due to their combined weight, which is (M+m)g (where M is the mass of the chair).
- Reaction: The floor exerts an equal and opposite force upward on the chair, which is also (M+m)g.
- Action: The chair exerts a downward gravitational force on the Earth due to its weight, which is (M+m)g.
- Reaction: The Earth exerts an equal and opposite force upward on the chair.
- Action: The boy exerts a downward gravitational force on the Earth due to his weight, which is mg.
- Reaction: The Earth exerts an equal and opposite force upward on the boy.
1. Boy → Chair: Downward force mg (Action)
- Chair → Boy: Upward force mg (Reaction)
2. Chair → Floor: Downward force (M+m)g (Action)
- Floor → Chair: Upward force (M+m)g (Reaction)
- Earth → Chair: Upward force (M+m)g (Reaction)
- Earth → Boy: Upward force mg (Reaction)
Topper's Solved these Questions
- THE FORCESBOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Exercises
12 Videos
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMA ENGLISHCHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - All Questions
75 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer
7 Videos
Similar Questions
STATEMENT -1 : Action and reaction acting on a particle cancels each other .
STATEMENT -2 : Action and reaction pair acts on different particles .
STATEMENT -3 : If an object is placed on a table then normal reaction by the table and weight are action reaction pair and they cancel each other .
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
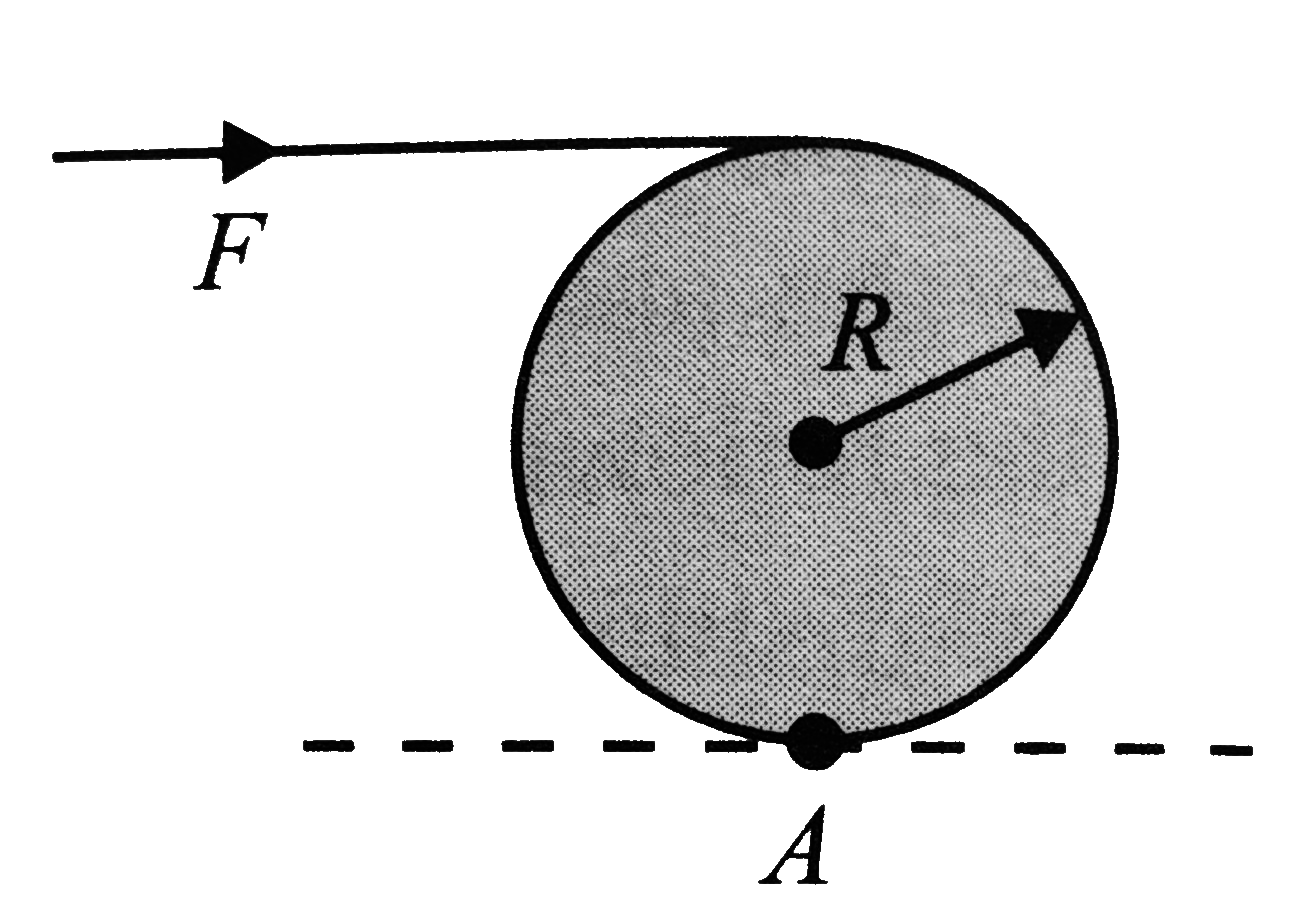
Component of reaction at the hinge in the horizontal direction is
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
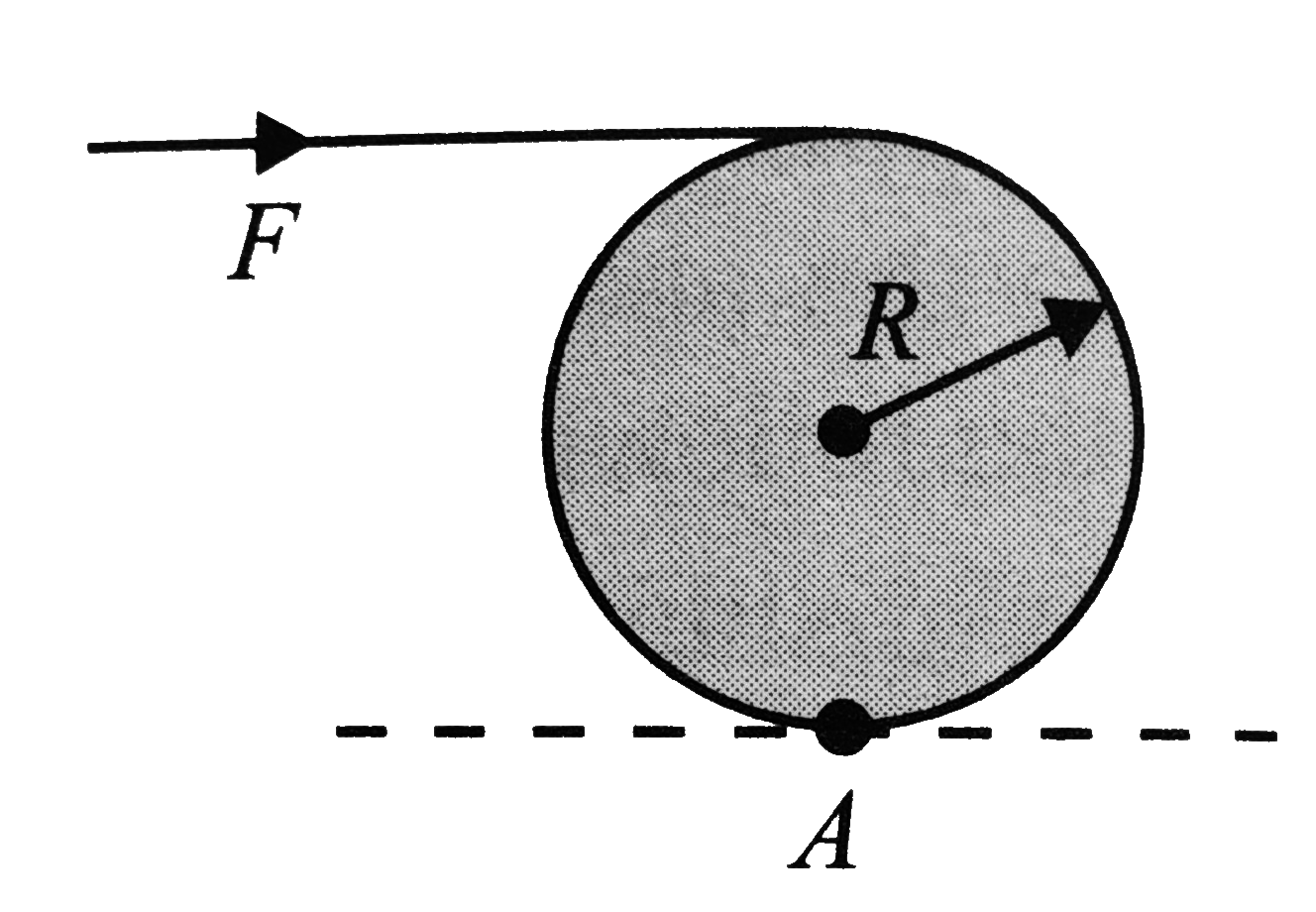
Component of reaction at the hinge in the vertical direction is
View SolutionThe block of mass m is in equilibrium relative to the smooth wedge of mass M which is pushed by a horizontal force F. Find pseudo force acting on (a) m, (b)M as viewed by the observer sitting on the wedge. Will these pseudo forces (c ) equal and opposite, action reaction pairs? Explain.

View SolutionAssertion :− A block is hanged from spring. Spring force on block gravitational force on block are not action and reaction pair.
Reason :− Action and reaction force acts in opposite direction.
View SolutionWhen a person is in a lift accelerated upwards or downwards, do force of gravity and normal reaction on the person form action and reaction pair?
View SolutionDraw a plot of potential energy of a pair of nucleons as a function of their separation . Write two important conclusions which you can draw regarding the nature of nuclear forces .
View SolutionA wooden block of mass 2 kg rests on a soft horizontal floor . When aniron cylinder of mass 25 kg is placed on top of the block , the floor yields steadily , and the block and the cylinder go down with an acceleration of 0.1ms−2 What is the action of the block on the floor (a) before and (b) after the floor yields ? Take g=10ms−2 . Identify the action reaction pairs in the problem .
View Solution
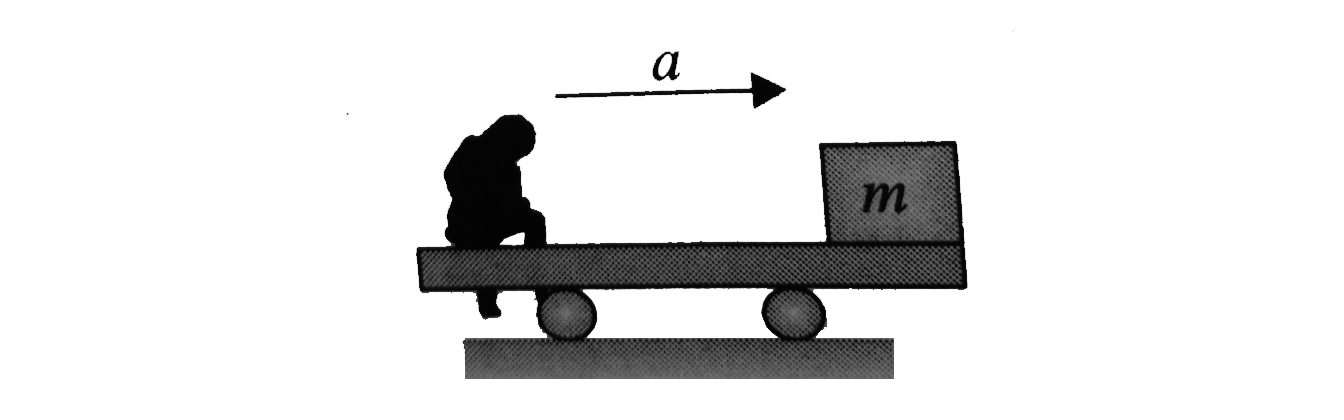
Suppose you are sitting on an accelrating trolley car.
(i) Find the pseudo force action on the block of mass m placed on the trolley car.
If the block is placed (or moved) outside the trolley car, and an external force F acts in horizontal direction.
(ii) Find the pseudo force acting on the block as viewed by the observer.
(iii) Find the acceleration of the block as seen by the obersever
View SolutionA 5 kg block is placed on the top of a 15 kg block as shown in figure . A horizontal force of 60 N is applied to the 15 kg block and the 5kg block is tied to the wall . The coefficient of friction between moving surfaces is 0.2

(a) Draw the free body diagram for each block w.r.t ground and identify the action reaction forces between two blocks .
(b) Determine the tension in the string and magnitude of the acceleration of the 15 kg block .
View Solution
