The centre of mass of a system of particles is at the origin. It follows that:
the number of particle to the righ of the origin is equal to the number of particles to the left
the total mass of the particles to the right of the origin is same as the total mass to the left of theorigin
the number of particles on X-axis should be equal to the number of particles on Y-axis
if there is a particle on the positive X-axis, there must be at least one particle on the negative X-axis.
To solve the problem, we need to analyze the implications of the center of mass (COM) being at the origin (0,0) for a system of particles.
1. Understanding Center of Mass:
The center of mass of a system of particles is defined as the point where the total mass of the system can be considered to be concentrated. Mathematically, the center of mass (COM) for a system of particles is given by:
Rcm=1M∑imiri
where M is the total mass, mi is the mass of the ith particle, and ri is the position vector of the ith particle.
2. COM at the Origin:
If the center of mass is at the origin, it implies:
∑imixi=0and∑imiyi=0
This means that the weighted sum of the positions of the particles must balance out to zero.
3. Analyzing the Options:
- Option 1: The number of particles to the right of the origin is equal to the number of particles to the left.
- This is incorrect because the center of mass depends on mass, not merely on the number of particles.
- Option 2: Total mass of the particles to the right of the origin is the same as the total mass of the particles to the left of the origin.
- This condition alone does not guarantee that the center of mass is at the origin; it only indicates balance along the y-axis.
- Option 3: The number of particles on the X-axis should be equal to the number of particles on the Y-axis.
- This is also incorrect because the center of mass is not determined by the count of particles in different axes.
- Option 4: If there is a particle on the positive x-axis, there must be at least one particle on the negative x-axis.
- This is correct. For the x-coordinate of the center of mass to be zero, if there is a positive contribution from a particle on the positive x-axis, there must be a corresponding negative contribution from a particle on the negative x-axis.
4. Conclusion:
Therefore, the correct option is Option 4.
The center of mass of a system of particles is defined as the point where the total mass of the system can be considered to be concentrated. Mathematically, the center of mass (COM) for a system of particles is given by:
Rcm=1M∑imiri
where M is the total mass, mi is the mass of the ith particle, and ri is the position vector of the ith particle.
If the center of mass is at the origin, it implies:
∑imixi=0and∑imiyi=0
This means that the weighted sum of the positions of the particles must balance out to zero.
- Option 1: The number of particles to the right of the origin is equal to the number of particles to the left.
- This is incorrect because the center of mass depends on mass, not merely on the number of particles.
- Option 2: Total mass of the particles to the right of the origin is the same as the total mass of the particles to the left of the origin.
- This condition alone does not guarantee that the center of mass is at the origin; it only indicates balance along the y-axis.
- Option 3: The number of particles on the X-axis should be equal to the number of particles on the Y-axis.
- This is also incorrect because the center of mass is not determined by the count of particles in different axes.
- Option 4: If there is a particle on the positive x-axis, there must be at least one particle on the negative x-axis.
- This is correct. For the x-coordinate of the center of mass to be zero, if there is a positive contribution from a particle on the positive x-axis, there must be a corresponding negative contribution from a particle on the negative x-axis.
Therefore, the correct option is Option 4.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
At one instant, the centre of mass of a system of two particles is located on the x-axis at x=3.0m and has a velocity of (6.0m/s)ˆj. One of the particles is at the origin, the other particle has a mass of 0.10kg and is at rest on the x−axis at x=12.0m.
(a) What is the mass of the particle at the origin?
(b) Calculate the total momentum of this system.
(c) What is the velocity of the particle at the origin?
View SolutionThe center of mass of a system of two particles divides the distance between them.
View Solution
Knowledge Check
The centre of mass of a system of two particle of masses m1andm2 is at a distance d1 from mass m1 and at a distance d2 from mass m2 such that.
Ad1d2=m2m1Bd1d2=m1m2Cd1d2=m1m1+m2Dd1d2=m2m1+m2Centre of mass of three particles of masses 1kg,2kgand3kg lies at the point (1,2,3) and centre of mass of another system of particles 3kgand2kg lies at the point (−1,3,−2). Where should we put a particle of mass 5kg so that the centre of mass of entire system lies at the centre of mass of first system ?
A(0, 0, 0)B(1, 3, 2)C(-1, 2, 3)D(3, 1, 8)
The center of mass of a system of two particles divides the distance between them.
View SolutionCalculate centre of mass of the system
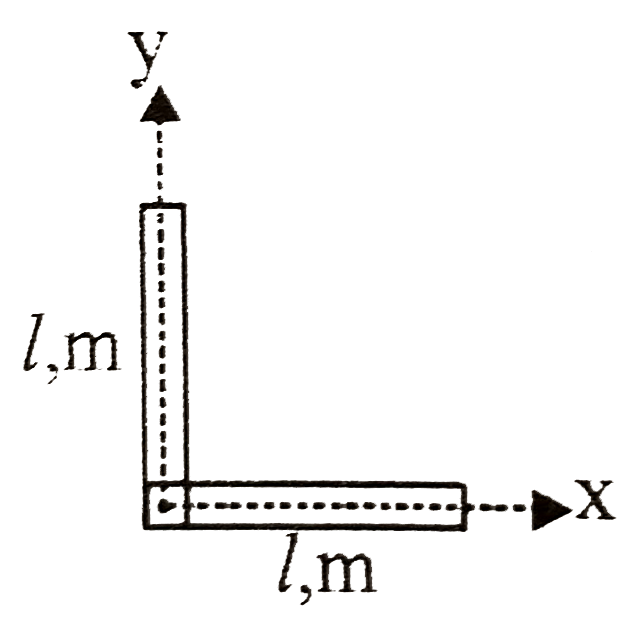
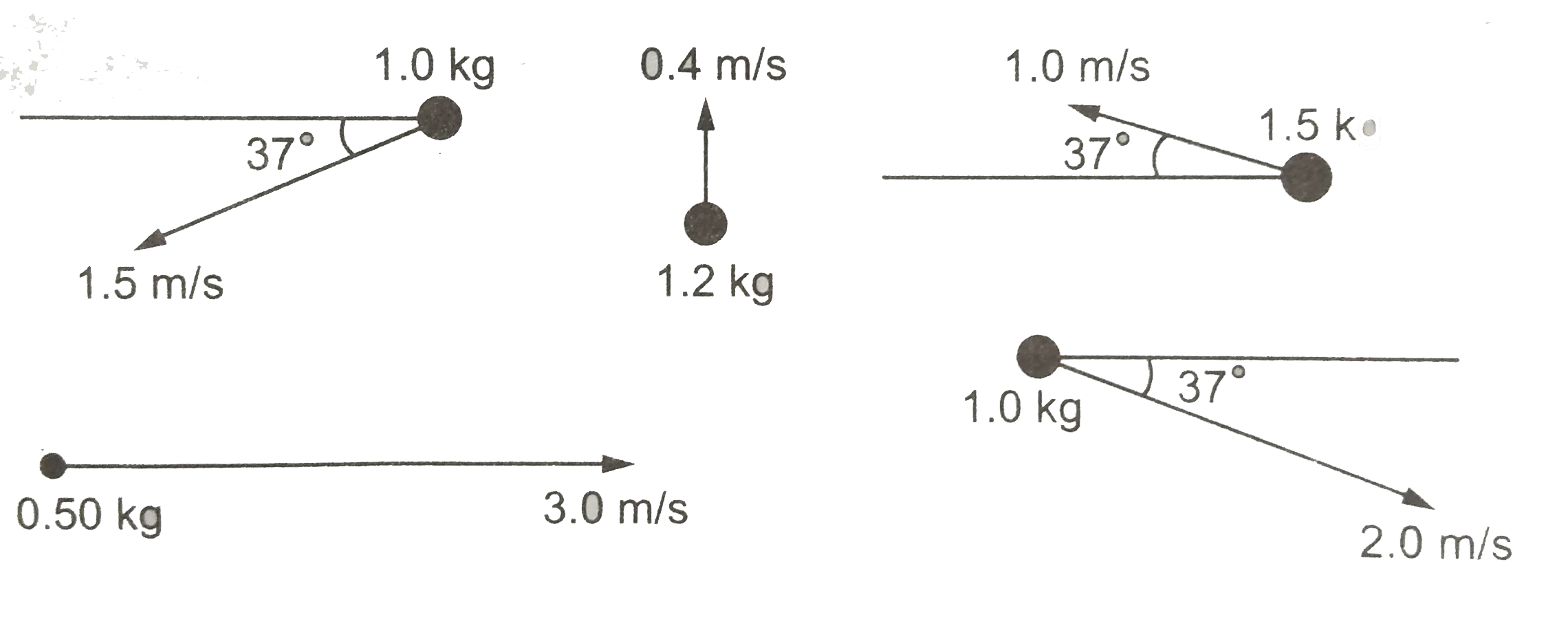
View SolutionCalculate the velocity of the centre of mss of the system of particles shown in figure.
View SolutionThe position of center of mass of a system of particles does not depend upon the
View SolutionThe position of centre of mass of system of particles at any moment does not depend on.
View SolutionThe position co-ordinates of the centre of mass of a system of three particles of equal masses which are placed on the verctices of an equilateral triangle of a side a are shown. Locate centre mass?

View Solution
