A sphere of mass m rolls without slipping on an inclined plane of inclination θ. Find the linear acceleration of the sphere and the force of friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?
Suppose the radils f the sphere is r. The forces acting on the sphere are shown in ure. They are a weight mg, b. normal force N and c. friction f.
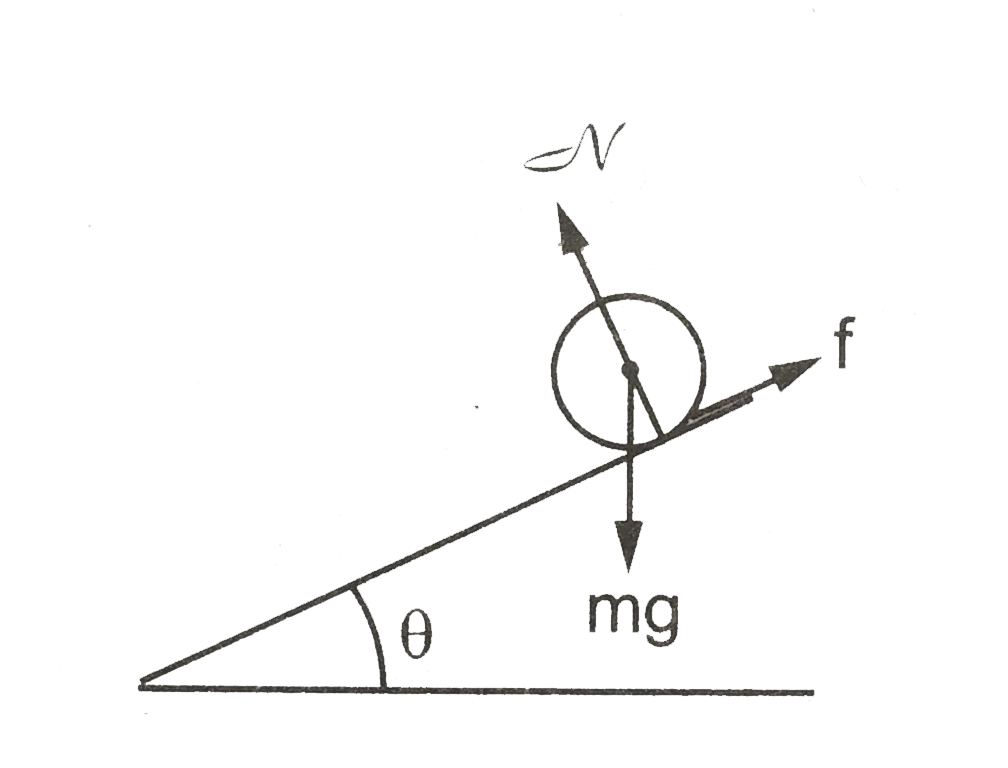
Let the linear acceleration of the sphere down the plane be a. The equation for the linear motion of the centre of mass is
mgsinθ−f=ma.............i
As the sphere rolls without slipping, its angular acceleration about the centre is ar.TheequationofrotatioNAlmotionaboutthecentreofmassis<br>fr=(2/5mr^2)(a/r)<br>or, f=2/5ma............ii<br>omiandii<br>a=5/7g sin theta<br>andf=27mgsinθ
The normal force is equal to mgcosθ as there is no acceleration perpendicular to the incline. The maximum friction that can act is therefore, μcosθ,whereμ is the coefficient of static friction. Thus, for pure rolling
μcosθ>27mgsinθ
or μ>27tanθ
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Objective -1
Explore 26 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Objective -2
Explore 14 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Question for short Answer
Explore 13 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Question for short Answer
Explore 15 Videos
Similar Questions
A solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionA sphere rolls down on an inclined plane of inclination θ. What is the acceleration as the sphere reaches bottom?
View SolutionA rolling object rolls without slipping down an inclined plane (angle of inclination θ), then the minimum acceleration it can have is ?
View SolutionA sphere rolls down on an inclied plane of inclination θ. What is the acceleration as the sphere reaches bottom ?
View SolutionA solid sphere of mass m rolls without slipping on an inlined plane of inclination 0. what shoul be the minimum coefficient of static feiction to support pure rolling?
View SolutionWhen a body rolls without sliding up an inclined plane the frictional force is :
View SolutionA sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
View SolutionA hollow sphere rolls without slipping down a plane inclined at an angle of 30° to the horizontal. Its linear acceleration will be
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View SolutionA hollow sphere of mass m starting from rest rolls without slipping, on an inclined plane of inclination What is the total energy of the sphere after 10−5s if after 10−5isv?
View Solution