The spring as shown in figure is kept in a stretched position with extension Xo when the system is released. Assuming the horizontal surface to be frictionless, the frequency of oscillation is

Considerign the two blocks plus the spring as a system, there is o exterN/Al resultant force on the system. Hence the centre of mass of the system will remain at rest. tE mean positions of the two simple harmonic motions occur whe the spring becomes unstretched. If the mass m moves towasrds right through a distance x and the mass M moves towards left through a distance X before the spring acquires N/Atural lenght
x+X=x0.............i
x and X will be the amplitudes of the two blocks m and M respectively. As the centre of mass should not change during the motion, we should also have
mx=MX............ii ltbrogt From i and ii x=Mx0M+mandX=mx0M+m
Hence the left block is x=Mx0M+m distance away from its mean position in the beginning of the motion. the force by the spring on this block at this instant is equal to the tension of spring
T=kx0
Now x=Mx0M+mor,x0=M+mMx
Thus,T=k(M+m)Mxor,a=Tm=k(M+m)Mmx
Theanga––requencyis∴omega=(sqrt(k(M+m))/(Mm))<br>andtheequencyisv=omega/(2pi)=1/(2pi)(sqrt((M+m))/(Mm))
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
The spring as shown in figure is kept in a stretched position with extension x when the system is relesed. Assuming the horizontal surface to be frictionless, the frequency of oscillation is

View SolutionIn the reported figure, two bodies A and B of masses 200 g and 800 g are attached with the system of springs. Springs are kept in a stretched position with some extension when the system is released. The horizontal surface is assumed to be frictionless. The angular frequency will be ___________ rad/s when k = 20 N/m.
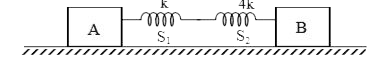
View Solution
Knowledge Check
The spring as shown in figure is kept in a stretched position with extension x when the system is released. Assuming the horizontal surface to be frictionless, the frequency of oscillation is
 A12π ⎷[k(M+m)Mm]B12π ⎷[mMk(M+m)]C12π√[kMm+M]D12π√[kmM+m]
A12π ⎷[k(M+m)Mm]B12π ⎷[mMk(M+m)]C12π√[kMm+M]D12π√[kmM+m]Assuming all the surfaces to be frictionless accelration of the block c shown in the figure is
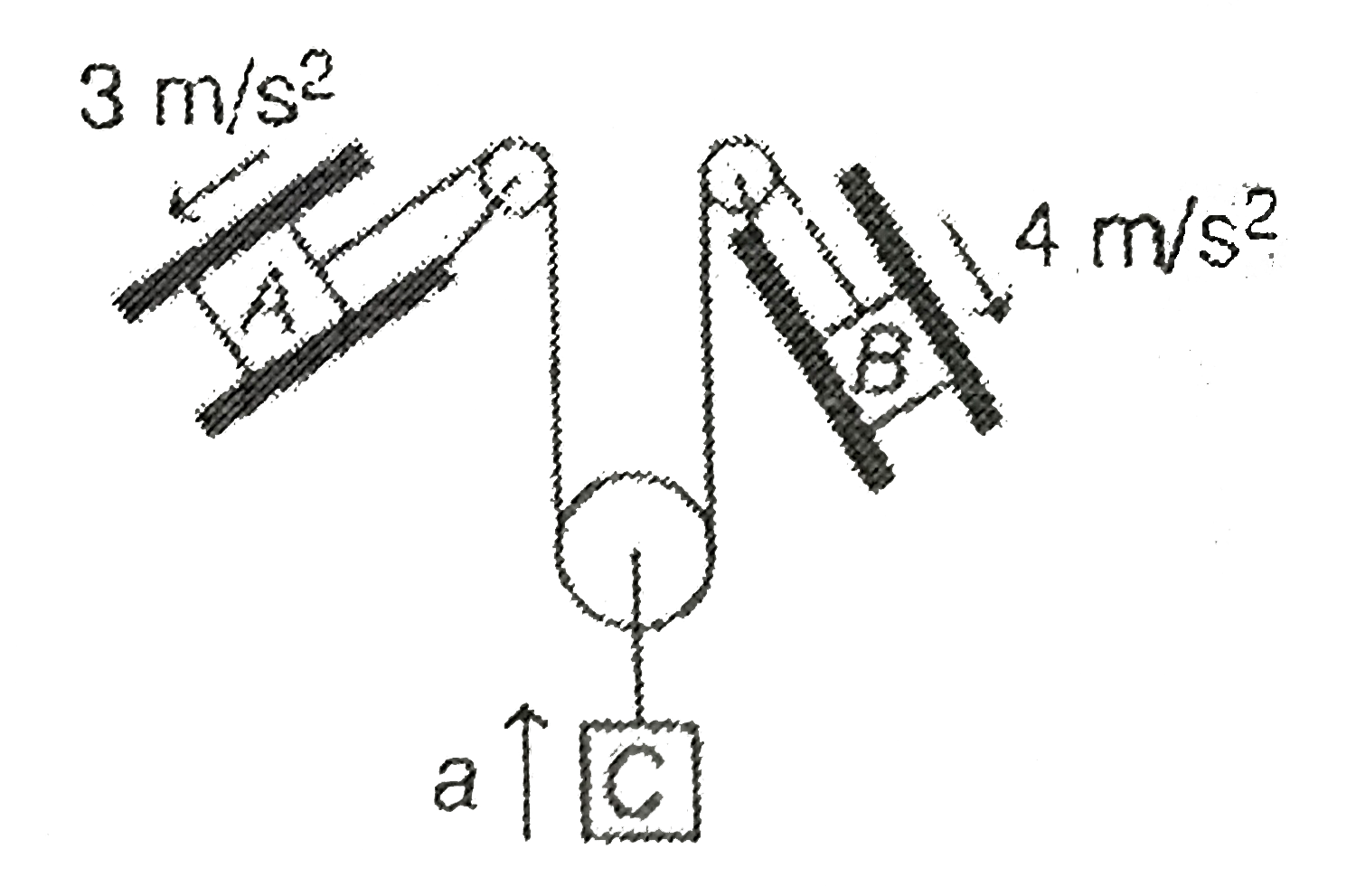 A5m/s2B7m/s2C3.5m/s2D4m/s2
A5m/s2B7m/s2C3.5m/s2D4m/s2A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
Assuming all the surfaces to be frictionless accelration of the block c shown in the figure is

View SolutionA system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?

View SolutionConsider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the puley, find the maximum eleongation of the spring.
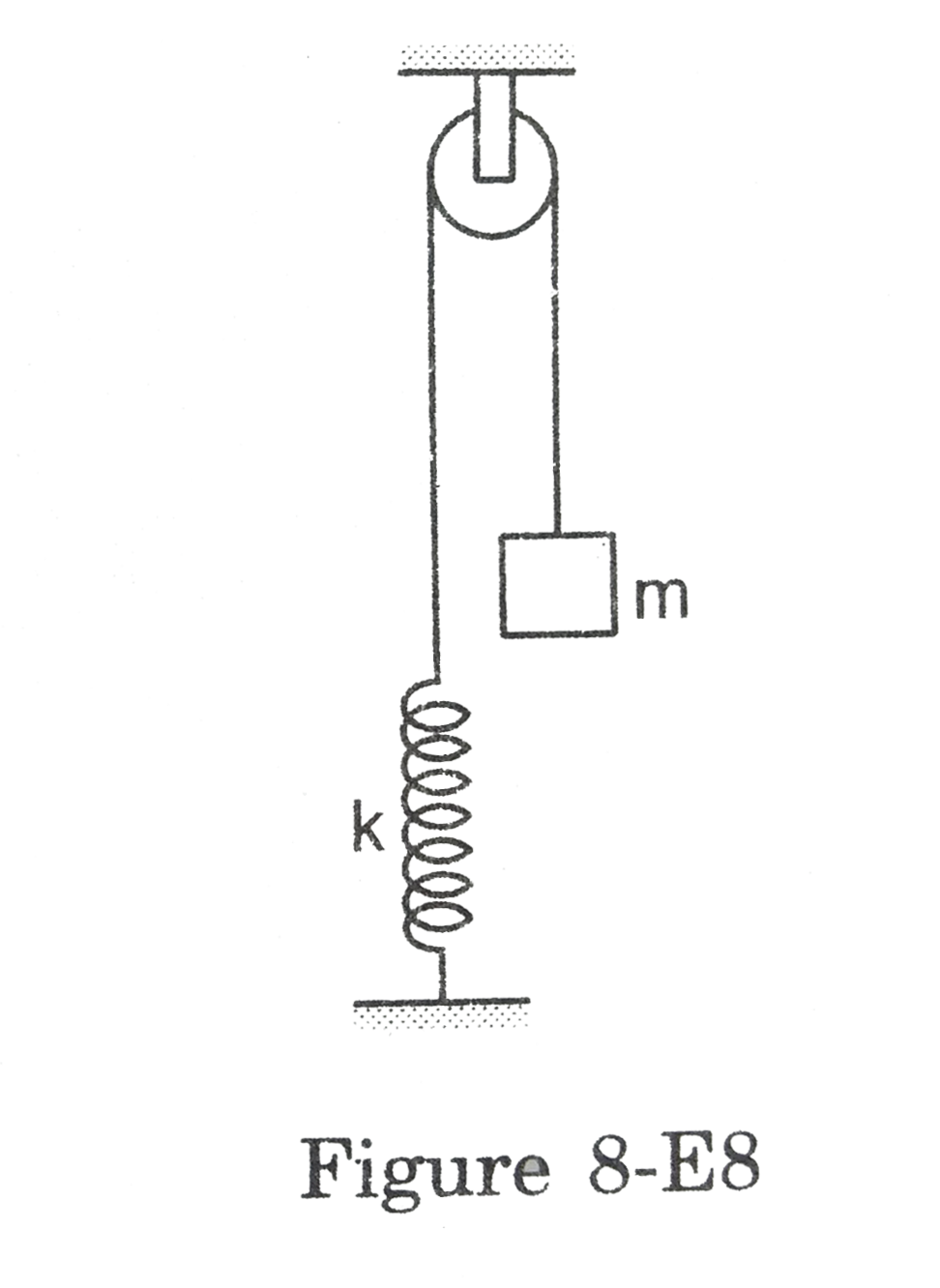
View SolutionConsider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the puley, find the maximum eleongation of the spring.

View SolutionA spring mass system oscillates in a car. If the car accelerates on a horizontal road, the frequency of oscillation will
View Solution
