A hollow sphere filled with water is used as the bob of a pendulum. Assume that the equation for simple pendulum is valid with the distance between the point of suspension and centre of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
To solve the problem, we need to analyze how the time period of a simple pendulum changes as water leaks out of a hollow sphere acting as the bob.
1. Understand the Formula for Time Period:
The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the effective length of the pendulum (the distance from the point of suspension to the center of mass of the bob) and g is the acceleration due to gravity.
2. Identify the Initial Condition:
Initially, when the hollow sphere is filled with water, the center of mass of the bob is at a certain position, which we can denote as L.
3. Effect of Water Leaking Out:
As water leaks out of the hollow sphere, the amount of water decreases, which causes the center of mass of the bob to shift downward. This results in an increase in the effective length L′ of the pendulum.
4. Analyze the Change in Time Period:
Since the effective length L′ increases as water leaks out, we can substitute L′ into the time period formula:
T′=2π√L′g
Because L′>L, it follows that T′>T. Therefore, the time period increases as water leaks out.
5. Final Condition:
Once all the water has leaked out, the hollow sphere is empty, and the center of mass returns to its original position. At this point, the effective length L′ returns to L, and the time period returns to its original value:
T=2π√Lg
6. Conclusion:
Thus, as water leaks out of the hollow sphere, the time period of the pendulum first increases and then returns to its original value once the sphere is empty.
Summary of Variations:
- As water leaks out: Time period increases.
- When the sphere is empty: Time period returns to original value.
The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the effective length of the pendulum (the distance from the point of suspension to the center of mass of the bob) and g is the acceleration due to gravity.
Initially, when the hollow sphere is filled with water, the center of mass of the bob is at a certain position, which we can denote as L.
As water leaks out of the hollow sphere, the amount of water decreases, which causes the center of mass of the bob to shift downward. This results in an increase in the effective length L′ of the pendulum.
Since the effective length L′ increases as water leaks out, we can substitute L′ into the time period formula:
T′=2π√L′g
Because L′>L, it follows that T′>T. Therefore, the time period increases as water leaks out.
Once all the water has leaked out, the hollow sphere is empty, and the center of mass returns to its original position. At this point, the effective length L′ returns to L, and the time period returns to its original value:
T=2π√Lg
Thus, as water leaks out of the hollow sphere, the time period of the pendulum first increases and then returns to its original value once the sphere is empty.
- As water leaks out: Time period increases.
- When the sphere is empty: Time period returns to original value.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
Knowledge Check
What is the effect on the time period of a simple pendulum if the mass off the bob is doubled?
AHalvedBDoubleCBecomes 8 timesDNo effects
A simple pendulum is made of bob which is a hollow sphere full of sand suspended by means of a wire. If all the sand is drained out, the period of the pendulum will
View SolutionThe period P of a simple pendulum is the time for one complete swing. How does P depend on the mass m of the bob, the length l of the string, and the acceleration due to gravity g?
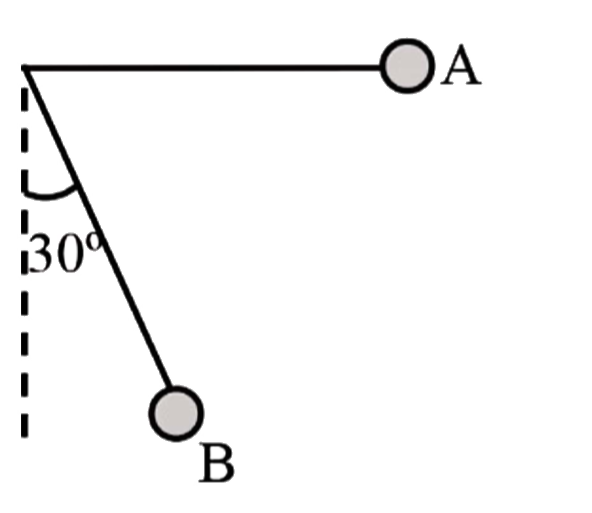
View SolutionA simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
View SolutionA simple pendulum of length 1 oscillates aboμt the mean position as shown in the figure. If the total energy of the pendulum is E, the velocity of the pendulum bob of mass m at point P is:
View SolutionState how does the time period of a simple pendulum depend on mass of bob.
View SolutionA hollow sphere is taken as bob of a simple pendulum. This hollow sphere is filled with fine sand. There is a small hole at the bottom of this sphere through which the fine sand leaks out. How does the time period of this simple pendulum alter? Discuss.
View SolutionThe time period of a simple pendulum in air is T. Now the pendulum is submerged in a liquid of density ρ16 where ρ is density of the bob of the pendulum. The new time period of oscillation is.
View Solution
