A piano wire weighing 6.00 g and having a length of 90.0 cm emits a fundamental frequency corresponding to the "Middle C" (v = 261.63 Hz). Find the tension in the wire.
The correct Answer is:1480N
To find the tension in the piano wire, we can follow these steps:
Step 1: Convert the mass of the wire to kilograms
The mass of the wire is given as 6.00 g. We need to convert this to kilograms since the standard unit of mass in physics is kilograms.
Mass (m)=6.00g=6.001000kg=0.006kg
Step 2: Convert the length of the wire to meters
The length of the wire is given as 90.0 cm. We need to convert this to meters.
Length (L)=90.0cm=90.0100m=0.9m
Step 3: Calculate the mass per unit length (μ)
Mass per unit length (μ) is calculated using the formula:
μ=mL
Substituting the values we have:
μ=0.006kg0.9m=0.0060.9kg/m=0.00667kg/m
Step 4: Use the formula for the fundamental frequency
The fundamental frequency (f) of a wire is given by the formula:
f=12L√Tμ
Where:
- f is the frequency (261.63 Hz)
- L is the length of the wire (0.9 m)
- T is the tension in the wire (which we need to find)
- μ is the mass per unit length (0.00667 kg/m)
Step 5: Rearrange the formula to solve for tension (T)
We can rearrange the formula to solve for T:
T=(2Lf)2μ
Step 6: Substitute the values into the equation
Now we can substitute the known values into the equation:
T=(2×0.9m×261.63Hz)2×0.00667kg/m
Calculating the term inside the parentheses first:
2×0.9×261.63=471.03
Now squaring this value:
(471.03)2=221,867.76
Now, substituting back to find T:
T=221,867.76×0.00667≈1470.00N
Final Answer
The tension in the wire is approximately:
T≈1470.00N
The mass of the wire is given as 6.00 g. We need to convert this to kilograms since the standard unit of mass in physics is kilograms.
The length of the wire is given as 90.0 cm. We need to convert this to meters.
Mass per unit length (μ) is calculated using the formula:
The fundamental frequency (f) of a wire is given by the formula:
- f is the frequency (261.63 Hz)
- L is the length of the wire (0.9 m)
- T is the tension in the wire (which we need to find)
- μ is the mass per unit length (0.00667 kg/m)
We can rearrange the formula to solve for T:
Now we can substitute the known values into the equation:
The tension in the wire is approximately:
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -29videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer9videos
THE FORCES
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
Similar Questions
The fundamental frequency of a sonometer wire increases by 6Hz if its tension is increased by 44% , keeping the length constant . Find the change in the fundamental frequency of the sonometer wire when the length of the wire is increased by 20% , keeping the original tension in the wire constant.
View SolutionThe fundatmental frequency of a sonometer wire increases by 6Hz if its tension is increased by 44% keeping the length constant. Find the change in the fundamental frequency of the sonometer when the length of the wire is increased by 20% keeping the original tension in the wire.
View SolutionA stretched wire is kept near the open end of a closed pipe 0.75 m long. The wire is 0.3 m long and has a mass of 0.01 kg. The wire is made to vibrate in its fundamental node, after Ixing at both ends. It sets the air column in the tube hito vibration at its fundamental frequency by resonance. Find (a) the frequency of oscillation of the air column and 6) the tension in the wire. Velocity of sound =330 m/s.
View SolutionA tube 1.0m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3m long and a mass of 0.01kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = 330m/s .View SolutionA piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire B produces 6 beats per second with it when the tension in A is slightly increased. Find the ratio of the tension in A to the tension in B.
View SolutionA piano wire with mass 3.00 g and length 80.0 cm is stretched with a tension of 25.0 N. A wave with frequancy 120.0 Hz and amplitude 1.6 mm travels along the wire. (a) calculate the average power carried by the wave. (b) what happenes to the avarage power if the wave amplitude is halved?
View SolutionIn a sonometer wire, the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has a volume of 0.0075 m 3. The fundamental frequency of the wire is 260 Hz . If the suspended mass is completely submerged in water, the fundamental frequency will become (take g=10ms−2) [
View SolutionA wire of length 40cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as 340m/s . Find the tension in the wire.
 View Solution
View SolutionConsider the situation shown in figure. The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 40ms−1, find the tension in the wire.
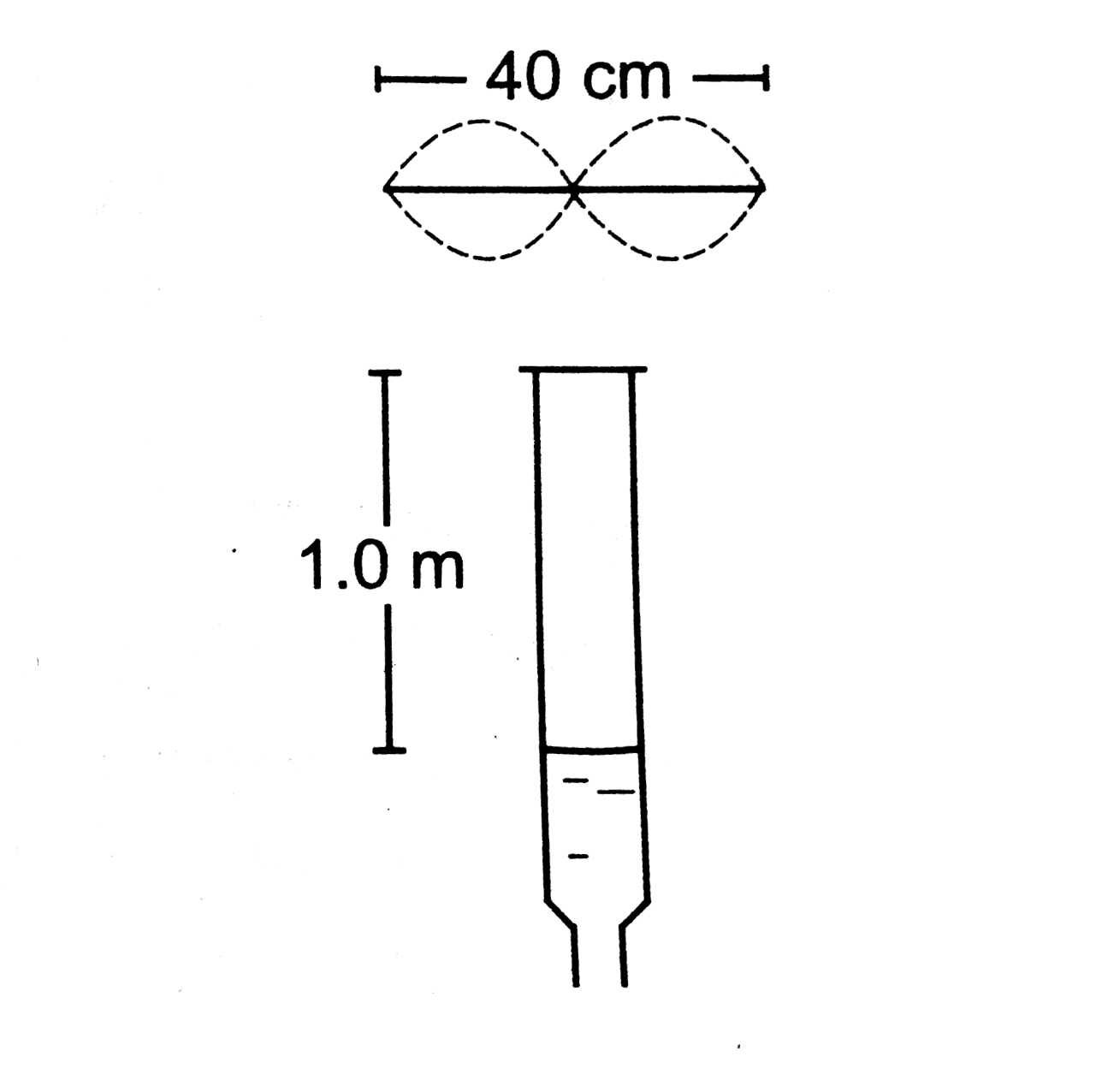 .View Solution
.View SolutionA wire of length 2.00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
View Solution

