A point source of light moves ijn a straight line paralel to a plane table. Consider a small portion of the table directly below the line of movement of the source. The illuminance at this portion varies with its distasnce r from the source as
The correct Answer is:C
To solve the problem, we need to analyze how the illuminance (E) at a point on the table varies with the distance (r) from the point source of light.
1. Understanding the Setup:
- We have a point source of light moving in a straight line parallel to a plane table.
- We consider a small portion of the table directly below the line of movement of the source.
2. Defining Variables:
- Let I be the intensity of the light source.
- Let r be the distance from the source to the point on the table directly below it.
- Let L be the constant distance from the source to the table.
3. Using the Illuminance Formula:
- The illuminance E at a point is given by the formula:
E=I⋅cos(θ)r2
- Here, θ is the angle between the line from the source to the point on the table and the vertical line from the source to the table.
4. Relating Angles:
- From the geometry of the situation, we can express cos(θ) in terms of L and r:
cos(θ)=L√L2+r2
5. Substituting into the Illuminance Formula:
- Substitute cos(θ) into the illuminance formula:
E=I⋅L√L2+r2r2
- This simplifies to:
E=ILr2√L2+r2
6. Analyzing the Relationship:
- As r increases, the term r2 in the denominator increases, which means E decreases.
- For large distances r compared to L, we can approximate √L2+r2≈r, leading to:
E≈ILr3
7. Conclusion:
- Thus, we find that the illuminance E is inversely proportional to r3:
E∝1r3
Final Answer:
The illuminance at the portion of the table varies with its distance r from the source as:
E∝1r3
- We have a point source of light moving in a straight line parallel to a plane table.
- We consider a small portion of the table directly below the line of movement of the source.
- Let I be the intensity of the light source.
- Let r be the distance from the source to the point on the table directly below it.
- Let L be the constant distance from the source to the table.
- The illuminance E at a point is given by the formula:
E=I⋅cos(θ)r2
- Here, θ is the angle between the line from the source to the point on the table and the vertical line from the source to the table.
- From the geometry of the situation, we can express cos(θ) in terms of L and r:
cos(θ)=L√L2+r2
- Substitute cos(θ) into the illuminance formula:
E=I⋅L√L2+r2r2
- This simplifies to:
E=ILr2√L2+r2
- As r increases, the term r2 in the denominator increases, which means E decreases.
- For large distances r compared to L, we can approximate √L2+r2≈r, leading to:
E≈ILr3
- Thus, we find that the illuminance E is inversely proportional to r3:
E∝1r3
The illuminance at the portion of the table varies with its distance r from the source as:
E∝1r3
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - question for short answer
13 Videos
- SEMICONDUCTOR AND SEMICONDUCTOR DEVICESBOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - Question for short answer
11 Videos
Similar Questions
A point charge is moving along a straight line with a constant velocity v. Consider a small area A perpendicular to the direction of motion of the charge . Calculate the displacement current through the area when its distance from the charge is x. The value of x is not large so that the electric field at any instant is essentially given by Coulomb's law.

View SolutionA point source emitting light uniformly in all directions is placed 60 cm above a table-top. The illuminance at a point on the table-top, directly below the source, is 15 lux. Find the illuminance at a point on the table-top 80 cm away from the first point.
View SolutionA point source emitting uniformly in all directions is placed above a table top at a distance of 0.50 m from it. The luminous flux of the source is 1570 lumen. Find the illuminance at a small surface area of the table to a.directly below the source and b. at as distance of 0.80 m from the source.
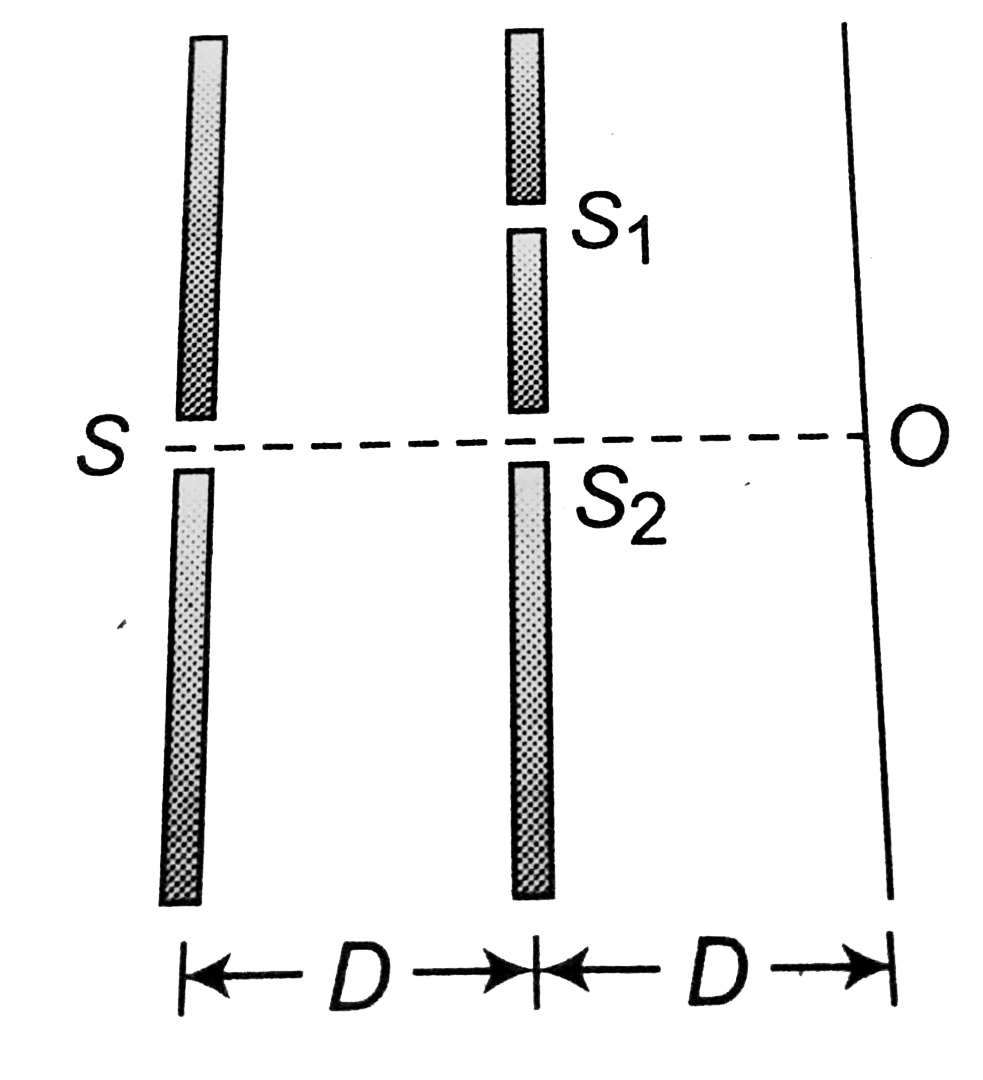
View SolutionTwo ideal slits S1 and S2 are at a distance d apart, and illuninated by light of wavelength λ passing through an ideal source slit S placed on the line through S2 as shown. The distance between the planes of slits and the source slit is D.A screen is held at a distance D from the plane of the slits. The minimum value of d for which there is darkness at O is (d<<D)
View SolutionA source of sound with natural frequency f0=1800Hz moves uniformly along a straight line separated from a stationary observer by a distance l=250m. The velocity of the source is equal to η=0.80 fraction of the velocity of the sound.
Q. The distance between the source and the observer at the moment when the observer receives a frequency f=f0 is

View SolutionA rectangular billiard table has vertices at P(0,0),Q(0,7),R(10,7), and S(10,0). A small billiard ball starts at M(3,4) , moves in a straight line to the top of the table, bounces to the right side of the table, and then comes to rest at N(7,1) . The y− coordinate of the point where it hits the right side is (a)3.7 (b) 3.8 (c)3.9(d) 4
View SolutionTwo coherent point sources S1andS2 emit light of wavelength λ. The separation between sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance on this line from S2 where a minimum of intensity occurs?
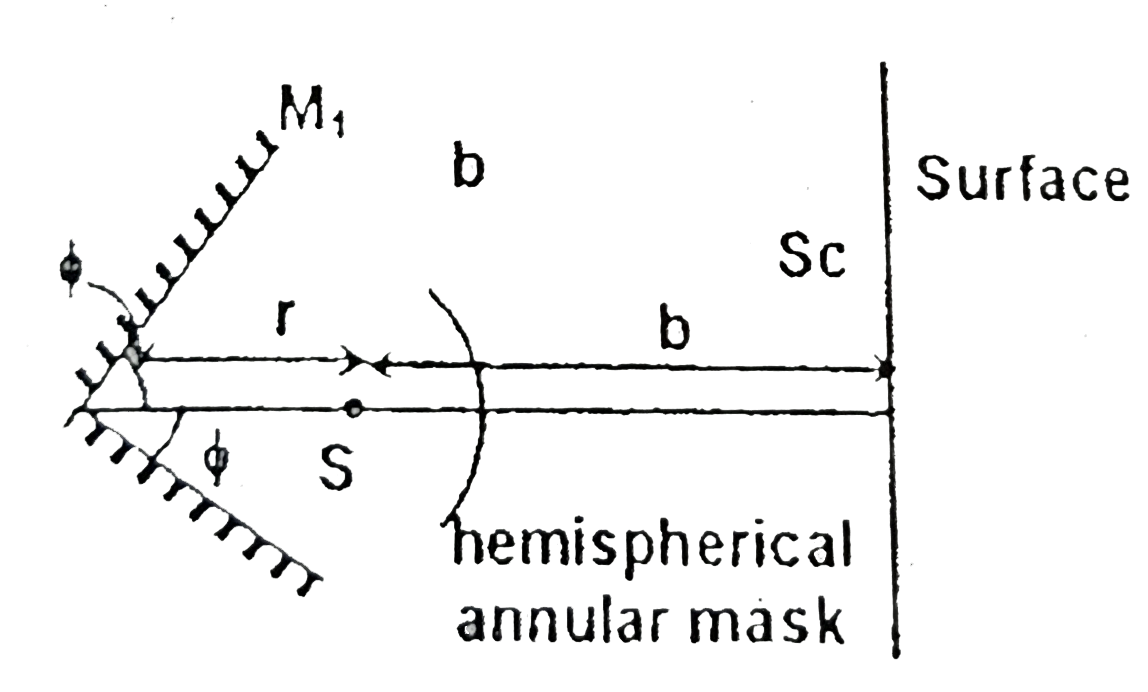
View SolutionTwo mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.
View SolutionA point source is placed at a depth h below the surface of water (refractive index = mu). (a) Show that light escapes through a circular area on the water surface with its centre directly above the point source. (b) Find the angle subtended by a radius of the area on the source.
View SolutionA point source of light is placed at a depth h=0.5 m below the surface of a liquid (μ=54) , Then , the fraction of light energy that escape directly from the liquid surface is
View Solution
