Let QandW denote the amount of heat given to an ideal gas and the work done by it in an adiabatic process.
Q=0
W=0
Q=W
Q≠W
The correct Answer is:A, D
To analyze the situation regarding an ideal gas undergoing an adiabatic process, we can follow these steps:
1. Understand the Adiabatic Process:
- In an adiabatic process, there is no heat transfer to or from the system. This means that the amount of heat Q given to the gas is zero.
- Therefore, we can conclude that:
Q=0
- This corresponds to Option 1.
2. Apply the First Law of Thermodynamics:
- The first law of thermodynamics states:
Q=ΔU+W
- Where ΔU is the change in internal energy and W is the work done by the gas.
- Since we established that Q=0, we can rewrite the equation as:
0=ΔU+W
- Rearranging gives us:
ΔU=−W
3. Analyze the Change in Internal Energy:
- For an ideal gas, the internal energy U is a function of temperature. If the gas undergoes an adiabatic process, there will be a change in temperature, which implies a change in internal energy:
ΔU≠0
- Since ΔU is not zero, it follows that W must also not be zero because of the relationship ΔU=−W. Therefore:
W≠0
- This means Option 2 is incorrect.
4. Evaluate the Relationship Between Q and W:
- We have established that Q=0 and W≠0.
- Therefore, Q is not equal to W:
Q≠W
- This means Option 3 is also incorrect, and Option 4 is correct.
5. Conclusion:
- The correct options are:
- Option 1: Q=0
- Option 4: Q≠W
Summary of Correct Options:
- Option 1: Q=0 (Correct)
- Option 4: Q≠W (Correct)
- In an adiabatic process, there is no heat transfer to or from the system. This means that the amount of heat Q given to the gas is zero.
- Therefore, we can conclude that:
Q=0
- This corresponds to Option 1.
- The first law of thermodynamics states:
Q=ΔU+W
- Where ΔU is the change in internal energy and W is the work done by the gas.
- Since we established that Q=0, we can rewrite the equation as:
0=ΔU+W
- Rearranging gives us:
ΔU=−W
- For an ideal gas, the internal energy U is a function of temperature. If the gas undergoes an adiabatic process, there will be a change in temperature, which implies a change in internal energy:
ΔU≠0
- Since ΔU is not zero, it follows that W must also not be zero because of the relationship ΔU=−W. Therefore:
W≠0
- This means Option 2 is incorrect.
- We have established that Q=0 and W≠0.
- Therefore, Q is not equal to W:
Q≠W
- This means Option 3 is also incorrect, and Option 4 is correct.
- The correct options are:
- Option 1: Q=0
- Option 4: Q≠W
- Option 1: Q=0 (Correct)
- Option 4: Q≠W (Correct)
Topper's Solved these Questions
Similar Questions
Knowledge Check
The work done in adiabatic process is given by
AnR(T1)−T2γBnR(T1)−T2γ−1C(nR(T1)−T2)RDγ(T1)−T2RnThe ideal gas equation for an adiabatic process is
APVγ=constantBTVγ+1=constantCPγ−1=constantDPγ+1T=constant
Find the value of molar heat capacity for an ideal gas in an adiabatic process.
View SolutionWhat is specific heat of a gas is an adiabatic process?
View SolutionIf Q, E and W denote respectively the heat added, change in internal energy and the work done in a closed cycle process, then
View SolutionThe ratio of work done by an ideal diatomic gas to the heat supplied by the gas in an isobatic process is
View SolutionThe figures given below show different processes (relating pressure P and volume V) for a given amount of an ideal gas. W is work done by the gas and ΔQ is heat absorbed by the gas.
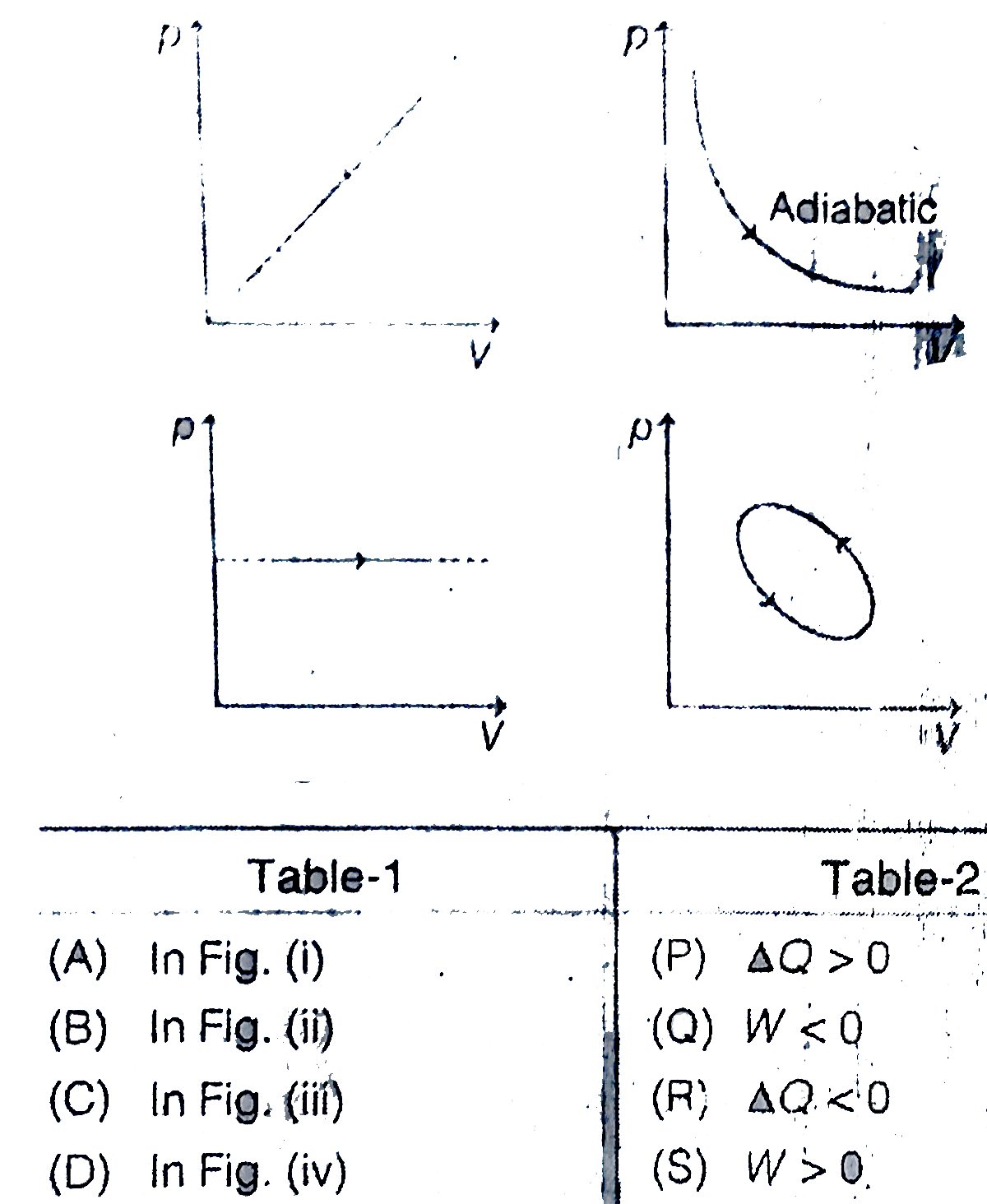
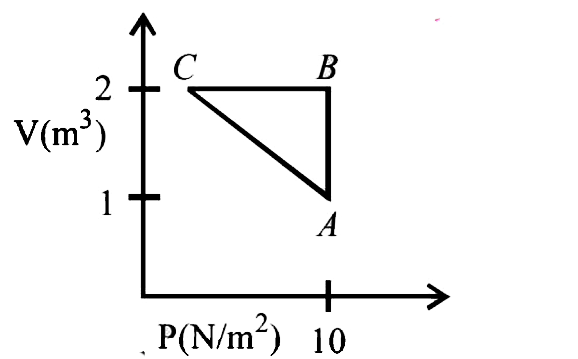
View SolutionAn ideal gas is taken through the cycle A→B→C→A, as shown in the figure, If the net heat supplied to the gas in the cycle is 5J, the work done by the gas in the process CtoA is
View Solution
