Apply the first law of thermodynamics to a resistor carrying a current i. Identify which of the quantities ΔQ, Delta U and DeltaW are zero, wheich are positive and which are negative.
To apply the first law of thermodynamics to a resistor carrying a current i, we can follow these steps:
Step 1: Understand the First Law of Thermodynamics
The first law of thermodynamics states:
ΔQ=ΔU+ΔW
where:
- ΔQ is the heat added to the system,
- ΔU is the change in internal energy of the system,
- ΔW is the work done by the system.
Step 2: Analyze the Resistor in the Circuit
Consider a resistor with resistance R connected to a battery providing a potential difference V. When a current I flows through the resistor, energy is dissipated in the form of heat.
Step 3: Determine the Work Done (ΔW)
In this scenario, the battery does work on the circuit to maintain the current. Thus, the work done by the battery is considered positive:
ΔW>0
Step 4: Determine the Heat (ΔQ)
As the current flows through the resistor, it generates heat due to the resistance. The heat generated can be expressed as:
ΔQ=I2RΔt
Since heat is generated in the resistor, we conclude:
ΔQ>0
Step 5: Determine the Change in Internal Energy (ΔU)
The internal energy of the resistor increases due to the heat generated. Since the temperature of the resistor rises as it dissipates heat, the change in internal energy is also positive:
ΔU>0
Summary of Quantities
- ΔQ (heat added to the system) is positive.
- ΔW (work done by the system) is positive.
- ΔU (change in internal energy) is positive.
Final Conclusion
In this case, all three quantities ΔQ, ΔW, and ΔU are positive.
---
The first law of thermodynamics states:
ΔQ=ΔU+ΔW
where:
- ΔQ is the heat added to the system,
- ΔU is the change in internal energy of the system,
- ΔW is the work done by the system.
Consider a resistor with resistance R connected to a battery providing a potential difference V. When a current I flows through the resistor, energy is dissipated in the form of heat.
In this scenario, the battery does work on the circuit to maintain the current. Thus, the work done by the battery is considered positive:
ΔW>0
As the current flows through the resistor, it generates heat due to the resistance. The heat generated can be expressed as:
ΔQ=I2RΔt
Since heat is generated in the resistor, we conclude:
ΔQ>0
The internal energy of the resistor increases due to the heat generated. Since the temperature of the resistor rises as it dissipates heat, the change in internal energy is also positive:
ΔU>0
- ΔQ (heat added to the system) is positive.
- ΔW (work done by the system) is positive.
- ΔU (change in internal energy) is positive.
In this case, all three quantities ΔQ, ΔW, and ΔU are positive.
Topper's Solved these Questions
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Exercise
24 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Short answer
2 Videos
- X-RaysBOOK - HC VERMA ENGLISHCHAPTER - X-RaysEXERCISE - Ques for Short Ans
10 Videos
Similar Questions
A process in which work perfomed by an ideal gas is proportional to the corresponding increment of its internal energy is described as a polytropic process. If we represent work done by a ppolytropic process by W and increase in internal energy as ΔU then
W∝ΔU
or W=K1ΔU ...(i)
For this process, it can be demonstrated that the relation between pressure and volume is given by the equation
PVη=K2 (constant ) .....(ii)
We know that a gas can have various values for molar specific heats. The molar specific heat 'C' for an ideal gas in polytropic process can be calculated with the help of first law of thermodynamics. In polytropic process process the variation of molar specific heat 'C' with η for a monatomic gas is plotted as in the graph shown.

For a monoatomic gas, the values of polytropic constant η for which value specific heat is negative.
View SolutionA process in which work perfomed by an ideal gas is proportional to the corresponding increment of its internal energy is described as a polytropic process. If we represent work done by a ppolytropic process by W and increase in internal energy as ΔU then
W∝ΔU
or W=K1ΔU ...(i)
For this process, it can be demonstrated that the relation between pressure and volume is given by the equation
PVη=K2 (constant ) .....(ii)
We know that a gas can have various values for molar specific heats. The molar specific heat 'C' for an ideal gas in polytropic process can be calculated with the help of first law of thermodynamics. In polytropic process process the variation of molar specific heat 'C' with η for a monatomic gas is plotted as in the graph shown.

In the graph shown, the y− coordinate of point A is ( for monatomic gas )
View SolutionAccording to the third law of thermodynamics which one of the following quantities for a perfectly crystalline solid is zero at absolute zero?
(a)Free energy
(b)Entropy
(c)Enthalpy
(d)Internal energy
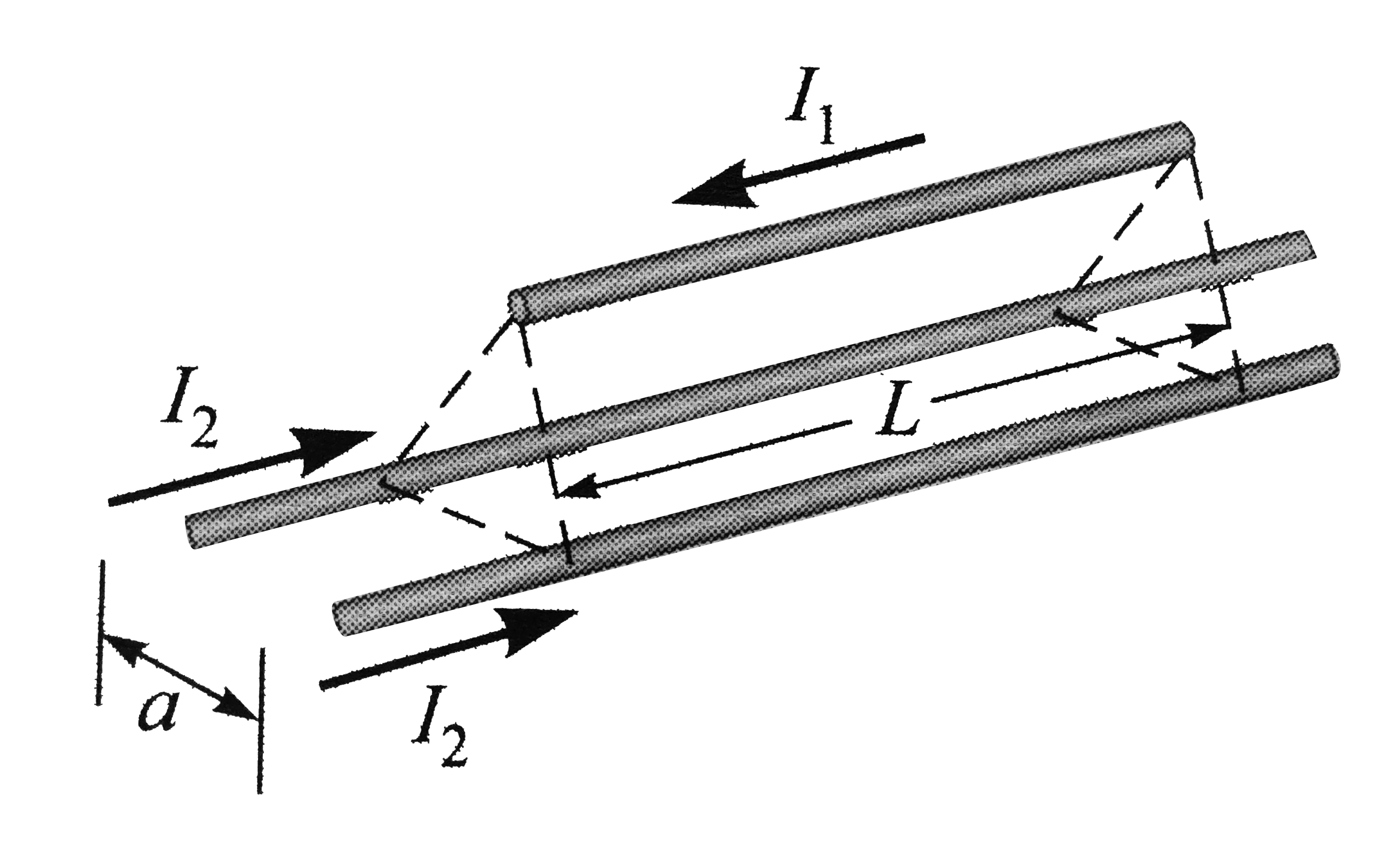
View SolutionTwo infinetely long, parallel wires are lying on the ground at distance a=1cm apart as shown in Fig. A third wire, of length L=10m and mass 400g, carries a current of I1=100A and is levitated above the first two wires, at a horizontal position midway between them. The infinitely long wires carry equal currents I1 in the same directions, but in the direction opposite that in the leviated wire. What current must the infinately long wires carry so that the three wires form an equilateral triangle?

View SolutionConsider the elements:
Cs,Ne,I and F
a. Identify the element that exhibits only negative oxidation state.
b. Identify the element that exhibits only positive oxidation state.
c. Identify the element that exhibits both positive and negative oxidation states.
d. Identify the element which exhibits neither the negative nor does the positive oxidation state.
View SolutionTwo long mutually perpendicular conductors carrying currents I1 and I2 lie in one plane, Find the locus of points at which the magnetic induction is zero.
View SolutionA circular coil of 100 turns and effective diameter 20cm carries a current of 0.5A. It is to be turned in a magnetic field of B=2.0T from a position in which the normal to the plane of the coil makes an angle θ equals to zero to one in which θ equals to 180∘. The work required in this process is
View SolutionThe current velocity of river grows in proportion to the distance from its bank and reaches the maximum value v0 in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.
View SolutionDepending on in which quadrant an angle θ lies, functions cosθ and sinθ may be positive or negative. In the second column of the given lable are specified whether these functions are positive or negative and in the first column are specified quadrants.
Column-IColumn-II(A) First(P)sinθ is positive(B) Second(Q)sinθ is negative(C) Third(R)cosθ is negative(D) Fourth(S)tanθ and sinθboth are negative(T)secθ is negative and sinθ is positive
View SolutionInfinite wires, each carrying a current 0.5 A, are kept parallel to y-axis and intersecting x-axis at x=±1 m, +02m, ±4m, ±8m etc. Wires kept at positive values of x carry current in the same direction while wires kept at negative values of x carry current successively in opposite directions as shown in Fig.
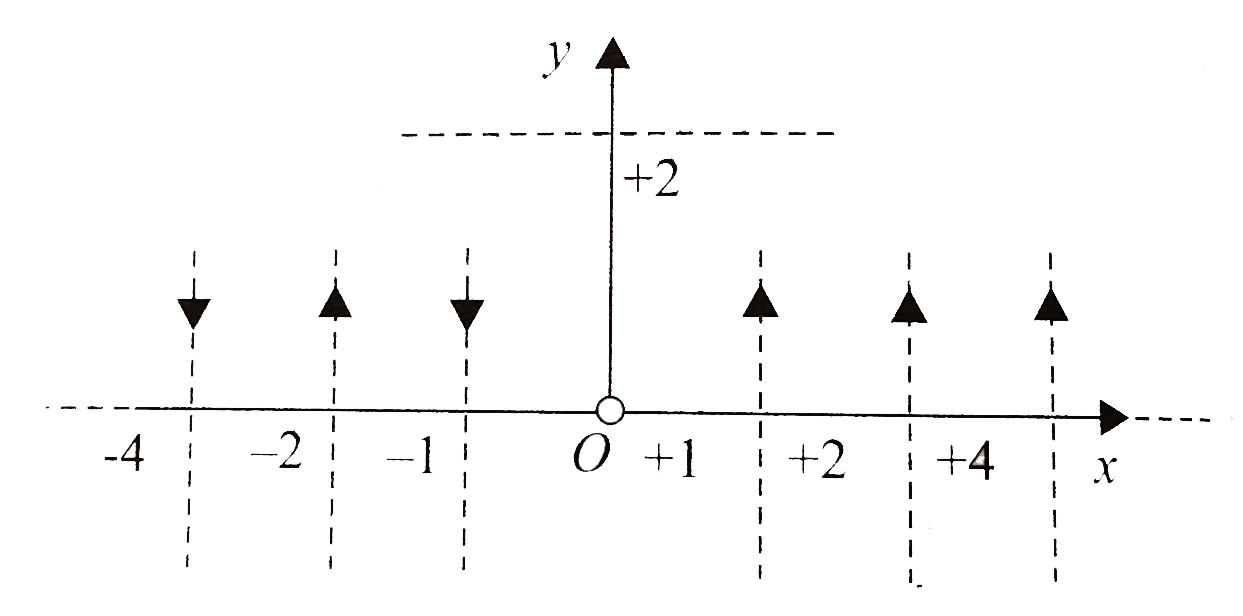
A wire is kept parallel to x-axis and intersecting y-axis at y=2 m. It carries a current i. Assuming this wire to be insulated from others then the current i in it such that magnetic induction at O is zero is
(assuming each wire to be infinitely long)
View Solution
