A beam of protons with a velocity of 4X105ms−1 enters a uniform magnetic field of 0.3 T. The velocity makes an angle of 60∘ with the magnetic field. Find the radius of the helical path taken by the proton beam.
The components of the proton's velocity along
and perpendicular to the magnetic filed are
v∣∣=((4×105ms−1cos60∘=2×105ms(−1).<br>andv_|_ = (4X10^5ms^(-1)) sin60^@ = 2sqrt3 X 10^5 ms^(-1).<br>Astheforce→qvX→Bisperpendica––r→themag≠ticfield,thecompo≠ntv_11willrema∈constant.INthepla≠perpendica––r→thefield,thepro→nwillequationqv_|_ B = (mv_|_^2)/(r) or, r = (mv_|_ )/(qB) = ((1.67X 10 ^(-27) kg)X (2sqrt3 X10^5ms^(-1)) /(1.6X 10^(-19) C) X (0.3T) ~~ 0.012m = 1.2 cm
. The time taken in one compete revolution in the plane perpendiuclar to B is T=(2pir)/(v_|_) = (2X3.14X0.12m )/ (2sqrt3 X 10^5 ms^(-1)
. The distance moved along the filed during this period, i.e., the pitch =(2X10^5ms^(-1) X2X3.14X 0.044m = 4.4cm.
The qualitative nature of the path of the protons is shown in figure.
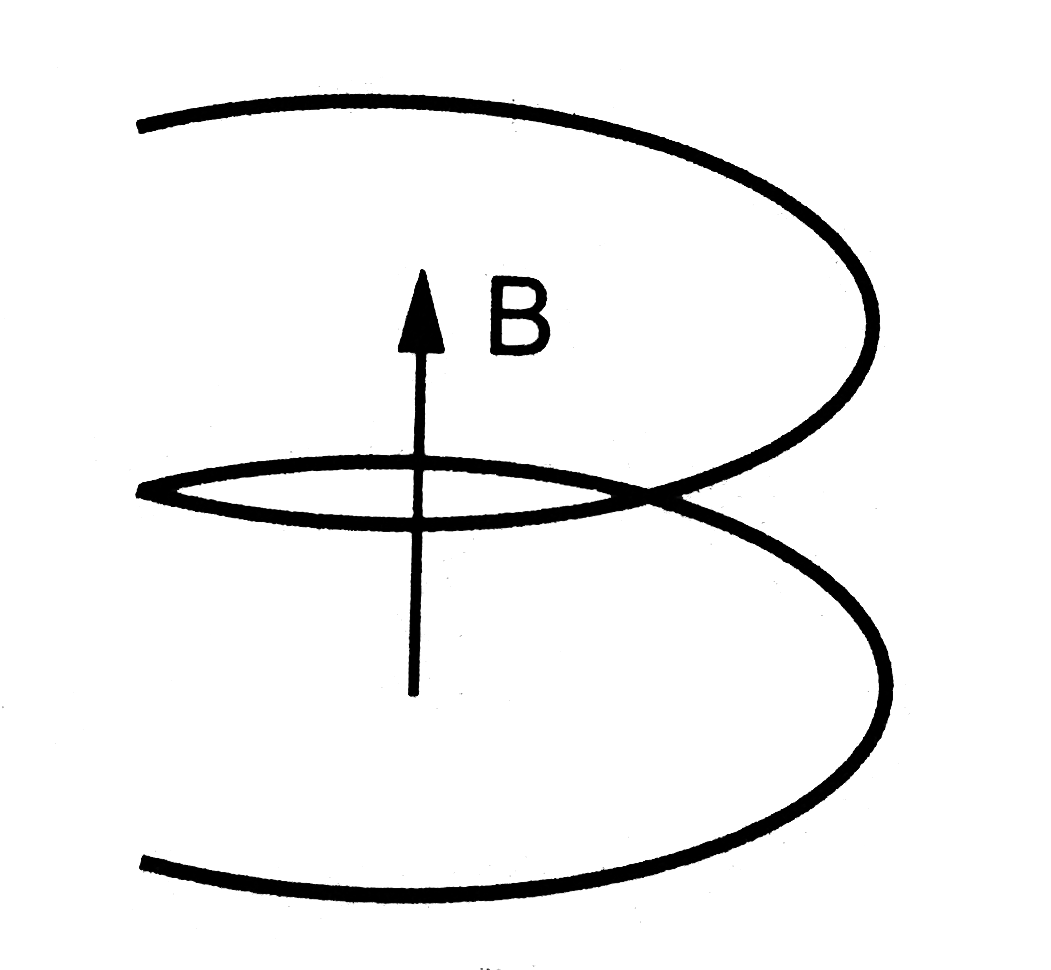
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 110videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - Exercises60videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
A beam of protons moving with a velocity of 4×105ms enters a uniform magnetic field of 0.3 T at an angle of 60◦ with the magnetic field. What is the radius of the helical path described by the proton beam?[mp=1.67×10−27kg and the charge on the proton=1.6×10−19C]
View SolutionA beam of protons with a velocity 4×105m/sec enters a uniform magnetic field of 0.4T at an angle of 37∘ to the magnetic field. Find the radius of the helical path taken by proton beam. Also find the pitch of helix.
sin37∘=3/5cos37∘=4/5. mp≅1.6×10−27kg.View Solution
Knowledge Check
- Question 1 - Select One
An electron having momentum 2.4×10−23 kg m s−1 enters a region of uniform magnetic field of 0.15 T. The field vector makes an angle of 30∘ with the initial velocity vector of the electron. The radius of the helical path of the electron in the field shall be
A2mmB1mmC√32 mmD0.5mm
A proton enter in a uniform magnetic field of 2.0 mT at an angle of 60degrees with the magnetic field with speed 10m/s. Find the picth of path
View SolutionA proton moving withh a velocity 2.5×107m/s enters a magnetic field of intensity 2.5T making an angle 30∘ with the magnetic field. The force on the proton is
View SolutionAn electron accelerated in an electric field of 20 kV enters a uniform magnetic field with induction 0.1 T. Its velocity vector makes an angle of 75∘ with the magnetic field vector. Find the shape of the path.
View SolutionA proton is projected with a velocity of 3X106ms−1 perpendicular to a uniform magnetic field of 0.6 T. find the acceleration of the proton.
View SolutionA charged particle enters a unifrom magnetic field with velocity vector at an angle of 45∘ with the magnetic field . The pitch of the helical path followed by the particles is ρ . The radius of the helix will be
View SolutionA beam of protons enters a uniform magnetic field of 0.3T with velocity of 4×105m/s in a direction making an angle of 60∘ with the direction of magnetic field. The path of motion of the particle will be
View SolutionA beam of ions with velocity 2×105 m/s enters normally into a uniform magnetic field of 4×10−2 T. if the specific charge to the ions is 5×107 C/kg, the radius of the circular path described will be
View Solution

