If the frequency of light in a photoelectric experiment is doubled the stopping potential will
be doubled
be halved
become more than double
become less than double
The correct Answer is:C
To solve the question regarding the effect of doubling the frequency of light on the stopping potential in a photoelectric experiment, we can follow these steps:
1. Understand the Photoelectric Effect: The photoelectric effect is described by Einstein's photoelectric equation:
hν=ϕ0+Kmax
where h is Planck's constant, ν is the frequency of the incident light, ϕ0 is the work function (threshold energy), and Kmax is the maximum kinetic energy of the emitted electrons.
2. Relate Kinetic Energy to Stopping Potential: The maximum kinetic energy can also be expressed in terms of stopping potential V0:
Kmax=eV0
where e is the charge of the electron. Thus, we can rewrite the equation as:
hν=ϕ0+eV0
3. Set Up the Equations for Two Cases:
- Case 1: Let the initial frequency be ν and the stopping potential be V0:
eV0=hν−ϕ0(Equation 1)
- Case 2: When the frequency is doubled to 2ν, let the new stopping potential be V′0:
eV′0=h(2ν)−ϕ0(Equation 2)
4. Express the New Stopping Potential:
From Equation 2:
eV′0=2hν−ϕ0
5. Divide the Two Equations:
To find the relationship between V′0 and V0, divide Equation 2 by Equation 1:
V′0V0=2hν−ϕ0hν−ϕ0
6. Simplify the Expression:
To simplify this, we can manipulate the numerator:
V′0V0=2hν−ϕ0hν−ϕ0=2(hν−ϕ0)+ϕ0hν−ϕ0
This can be rewritten as:
V′0V0=2+ϕ0hν−ϕ0
7. Analyze the Result:
Since for photoelectric emission to occur, hν must be greater than ϕ0 (i.e., hν>ϕ0), the term ϕ0hν−ϕ0 is positive. Therefore:
V′0V0>2
8. Conclusion:
This implies that the new stopping potential V′0 is greater than twice the original stopping potential V0. Thus, the correct answer is that the stopping potential will become more than double.
Final Answer:
The stopping potential will become more than double when the frequency of light in a photoelectric experiment is doubled.
---
hν=ϕ0+Kmax
where h is Planck's constant, ν is the frequency of the incident light, ϕ0 is the work function (threshold energy), and Kmax is the maximum kinetic energy of the emitted electrons.
Kmax=eV0
where e is the charge of the electron. Thus, we can rewrite the equation as:
hν=ϕ0+eV0
- Case 1: Let the initial frequency be ν and the stopping potential be V0:
eV0=hν−ϕ0(Equation 1)
- Case 2: When the frequency is doubled to 2ν, let the new stopping potential be V′0:
eV′0=h(2ν)−ϕ0(Equation 2)
From Equation 2:
eV′0=2hν−ϕ0
To find the relationship between V′0 and V0, divide Equation 2 by Equation 1:
V′0V0=2hν−ϕ0hν−ϕ0
To simplify this, we can manipulate the numerator:
V′0V0=2hν−ϕ0hν−ϕ0=2(hν−ϕ0)+ϕ0hν−ϕ0
This can be rewritten as:
V′0V0=2+ϕ0hν−ϕ0
Since for photoelectric emission to occur, hν must be greater than ϕ0 (i.e., hν>ϕ0), the term ϕ0hν−ϕ0 is positive. Therefore:
V′0V0>2
This implies that the new stopping potential V′0 is greater than twice the original stopping potential V0. Thus, the correct answer is that the stopping potential will become more than double.
The stopping potential will become more than double when the frequency of light in a photoelectric experiment is doubled.
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - objective II
7 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Exercise
35 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - work out
13 Videos
- PERMANENT MAGNETSBOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Short Answer
11 Videos
- PHOTOMETRYBOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions
38 Videos
Similar Questions
If the frequency of light in a photoelectric experiment is double then maximum kinetic energy of photoelectron
View SolutionA light beam containing a number of wavelengths is used in an photoelectric experiment. The stopping potential :
View SolutionAssertion: If frequency of incident light is doubled, the stopping potential will also become two times
Reason: Stopping potential is given by V0=he(v−v0)
View SolutionIn a photoelectric experiment, it was found that the stopping potential decreases from 1.85 V to 0.82 V as the wavelength of the incident light is varied from 300nm to 400nm. Calculate the value of the Planck constant from these data.
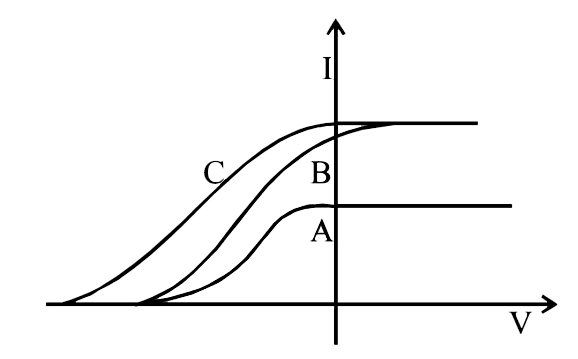
View SolutionIn a photoelectric experiment anode potential is ploted against plate current.
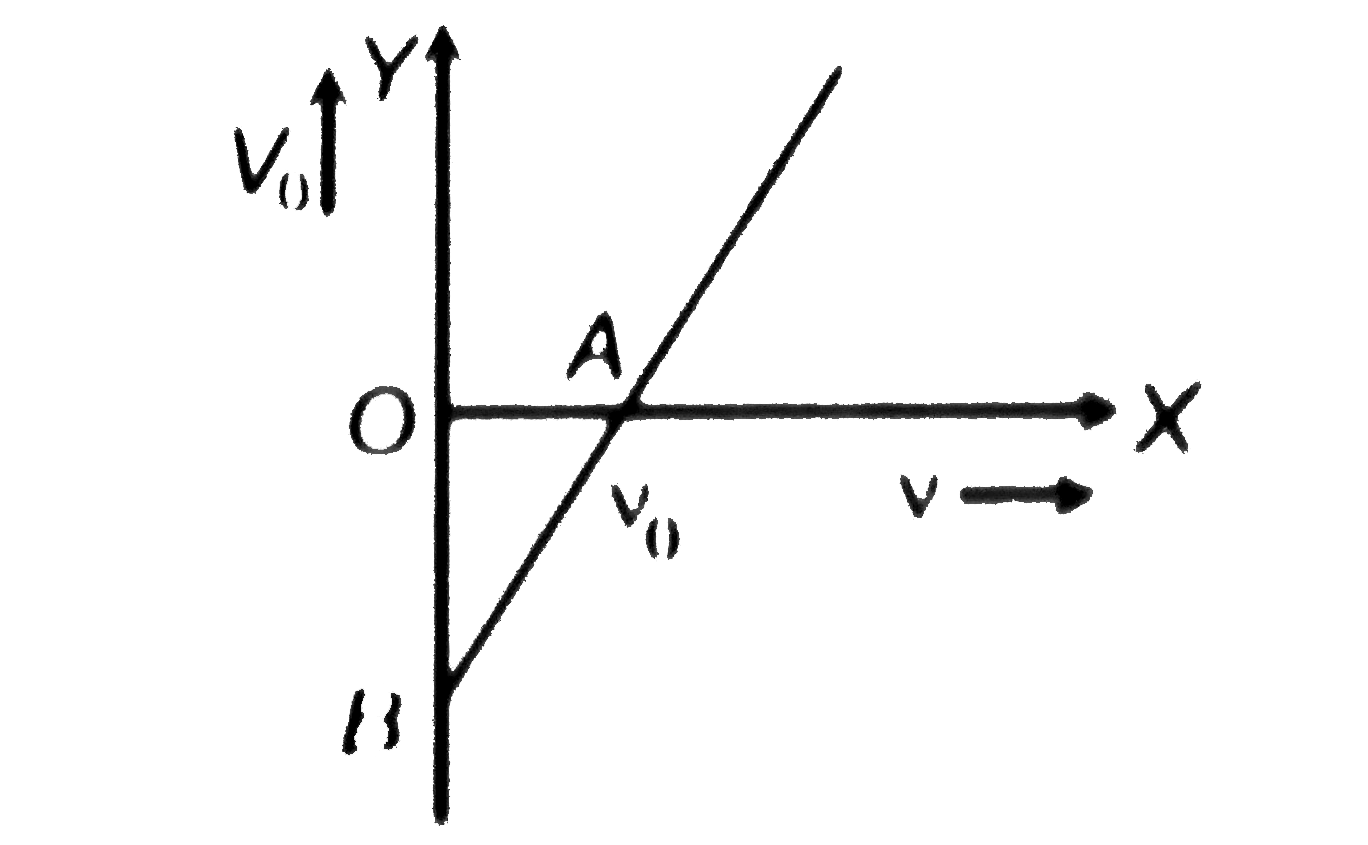
View SolutionIn an experiment on photoelectric effect the frequency f of the incident light is plotted against the stopping potential V0. The work function of the photoelectric surface is given by ( e is the electronic charge)
View SolutionLight of frequency 1.5 times the threshold frequency is incident on a photosensitive material, photo electric current is emitted. If the frequency of light is halved and intensity is doubled, the photoelectric current becomes
View SolutionIf the frequency of incident light is tripled, the stopping potential will
View SolutionThe threshold frequency for a certain photosensitive metal is v0. When it is illuminated by light of frequency v=2v0, the stopping potential for photoelectric current is V0. What will be the stopping potential when the same metal is illuminated by light of frequency v=3v0?
View SolutionKmax (in eV) = 3, and frequency of light (in Hz) =1×1015 for a metal used as a cathode in a photoelectric experiment. The threshold frequency of light for the photoelectric emission from the metal is -
View Solution
